Jeżeli kiedykolwiek gubiłeś się w gąszczu równań trygonometrycznych, nie martw się! Podstawowe wzory trygonometryczne, niczym magiczny klucz, otwierają drzwi do algorytmów równań. Zacznijmy od najpopularniejszych funkcji: sinus, cosinus i tangens. Te trzy różne "stworzenia" przypominają trójkę muszkieterów. Każde z nich posiada unikalne zdolności, jednak wszystkie działają na tej samej zasadzie. Można je rozwiązać za pomocą graficznych wykresów, które przypominają zawirowania tańca na parkiecie.
- Podstawowe wzory trygonometryczne (sinus, cosinus, tangens) są kluczowe w rozwiązywaniu równań trygonometrycznych.
- Równania sinusoidy i cosinus mają nieskończoną liczbę rozwiązań, które można uzyskać poprzez dodanie odpowiednich wielokrotności \(2\pi\).
- Metody graficzne ułatwiają zrozumienie równań, pozwalając na wizualizację przecięć wykresów, które wskazują rozwiązania.
- Równania trygonometryczne mają zastosowanie w wielu dziedzinach, takich jak budownictwo, nawigacja i sporty ekstremalne.
- Typowe pułapki w rozwiązywaniu równań to m.in. zbyt wczesne zniechęcenie, zapominanie o nieskończoności rozwiązań, ignorowanie dziedzin funkcji oraz brak cierpliwości.
- Kluczowe jest zrozumienie, że sinus i cosinus mają okres \(2\pi\) i mogą mieć wiele rozwiązań w danym przedziale.
Równanie sinusoidy - prosty krok do przodu!
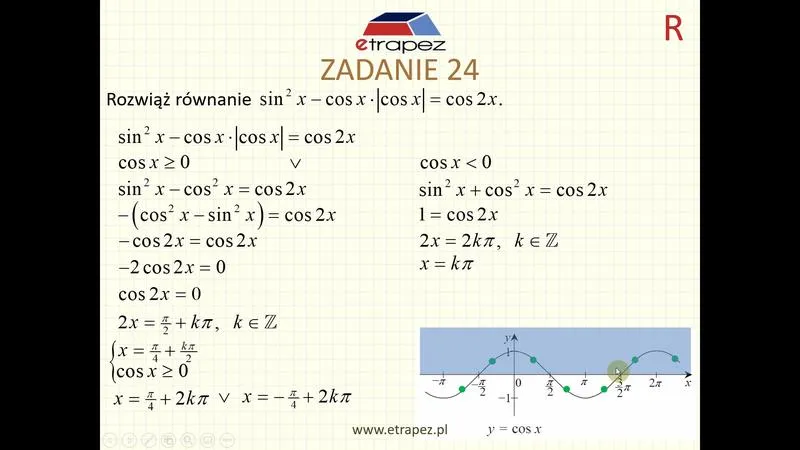
Przyjrzyjmy się równaniu, takim jak \( \sin x = a \). Oczywiście, wszystko działa prawidłowo jedynie wtedy, gdy \( a \) mieści się w granicach od -1 do 1. Rysując wykresy funkcji sinus oraz \( y = a \), zdobędziesz cenne wskazówki dotyczące miejsc, w których te dwie linie się przecinają. Pamiętaj, że sztuczka tkwi w tym, iż każdy kąt posiada nieskończoną liczbę rozwiązań, do których dodamy \( 2k\pi \), gdzie \( k \) to dowolna liczba całkowita. Wiesz, jak to mówią – im więcej, tym lepiej!
Cosinus - Twoja tajna broń!

Kolej na cosinus! Równanie \( \cos x = a \) działa na podobnej zasadzie. Kiedy \( a \) również mieści się w przedziale od -1 do 1, otrzymujesz pełne pole do działania! Podobnie jak w przypadku sinusa, rysując wykresy obu funkcji, odkrywasz, że tak naprawdę stajesz przed podwójnymi problemami do rozwiązania. Równanie to również dostarcza nieskończoną liczbę rozwiązań – możesz pisać \( 2k\pi \) lub \( -2k\pi \), w zależności od wybranej strony szczęścia!
Co jest najfajniejsze? Po opanowaniu podstawowych wzorów trygonometrycznych dostrzegasz, że kij od miotły zamienia się w różdżkę do magii matematycznej! Gdy dodasz do tego tangens i cotangens, zyskujesz kompletny zestaw narzędzi. Niektóre równania wydają się straszne, ale z pomocą tych przyjaciół możesz w mgnieniu oka wyczarować odpowiedzi. Dlatego zabierz kartkę i długopis, bo na uczcie trygonometrii czas na zabawę!
Metody graficzne w rozwiązywaniu równań trygonometrycznych
Rozwiązywanie równań trygonometrycznych z pewnością nie musi być nudne, jak przestarzały zeszyt pełen formuł matematycznych. Wręcz przeciwnie! Obecnie stosujemy metody graficzne, które znacząco angażują nas w ten proces, czyniąc go znacznie bardziej atrakcyjnym. Wystarczy połączyć odpowiednie funkcje, takie jak sinus i cosinus, a następnie obserwować, jak wspólnie układają się na wykresie. Dlaczego to takie fascynujące? Ponieważ każdy punkt przecięcia wykresów wskazuje potencjalne rozwiązania równań, a my możemy śmiało sięgnąć po ołówek i papier, żeby odnaleźć te „złote miejsca”, które odpowiadają na pytania, niczym w prawdziwym śledztwie kryminalnym!
Na początku procesu rysujemy wykresy. Na przykład w przypadku równania \( \sin x = a \) (gdzie a należy do przedziału od minus jednego do jednego), rysujemy obie funkcje: \(y = \sin x\) oraz \(y = a\). Pamiętajmy jednak, że jeżeli a przekracza ten przedział, możemy je zignorować, ponieważ rozwiązania stają się wówczas porównywalne do legendarnych jednorożców. Gdy znajdziemy punkt przecięcia, to czas na zabawę z serią rozwiązań – do naszego wyniku dodajemy 2kπ. Choć to łatwiej powiedzieć niż zrealizować, z odrobiną praktyki task staje się bułką z masłem!
Nie tylko sinus i cosinus
Przenieśmy teraz naszą uwagę do cosinusa! Równanie \( \cos x = a \) cechuje się podobnymi zasadami. Ponownie rysujemy wykresy, zidentyfikujemy punkty przecięcia, a następnie otwieramy drzwi do odkrywania nowych rozwiązań. Może być zaskakujące, ale dla cosinusa również otrzymujemy nieskończoną liczbę rozwiązań, co oznacza kolejne magiczne serie! W końcu, nikt nie powiedział, że trygonometria musi być monotonnie nudna, prawda?
Również w przypadku tangensa możemy napotkać ciekawe zwroty akcji. Tutaj rysujemy \(y = \tan x\), a w zasadzie każdy punkt przecięcia ze stałą linią \(y = a\) staje się szansą na znalezienie nowego rozwiązania. Musimy jednak zachować czujność! Pamiętajmy, że tangens ma swoje ograniczenia, a szczególnie musimy unikać miejsc, gdzie funkcja jest niewłaściwa, co oznacza, że \(x \neq kπ\).
Warto również znać kilka kluczowych faktów dotyczących tych funkcji:
- Sinus i cosinus mają okres 2π.
- Cosinus jest parzystą funkcją.
- Wartości tangensa są nieokreślone w miejscach kątów π/2 + kπ.
- Każda funkcja trygonometryczna może mieć nieskończoną liczbę rozwiązań w danym przedziale.
W końcu graficzne podejście do równań trygonometrycznych sprawia, że matematyka staje się prawdziwą zabawą, a my, jako detektywi, odkrywamy zagadki, które ona skrywa!
Przykłady zastosowania równań trygonometrycznych w zadaniach praktycznych
Równania trygonometryczne przypominają zaklęcia w matematycznym świecie – potrafią zdziałać cuda, jeśli tylko umiejętnie je zastosujemy! Wiele codziennych sytuacji, od budownictwa poprzez nawigację, pokazuje praktyczne zastosowanie tych równań. Na przykład, astronomowie korzystają z równań trygonometrycznych, aby obliczać odległości do gwiazd. W skrócie – w jednym momencie mamy możliwość policzenia, jak daleko znajduje się najbliższa galaktyka, a w drugim dokładamy fundamenty pod wymarzone patio, bazując na parametrach kątowych! To niezwykła wszechstronność!
Patrząc na projektowanie budynków, widzimy, jak istotne są równania trygonometryczne. Gdy architekt decyduje się na stworzenie nowej wieży, musi uwzględnić nie tylko jej wysokość, lecz także kąt nachylenia dachu. Właśnie tutaj równania trygonometryczne stają się nieocenioną pomocą! Dzięki obliczeniom funkcji sinus i cosinus architekt zyskuje pewność, jak stromy powinien być dach, aby zapobiec ześlizgiwaniu się śniegu i liści. Dzięki trygonometrii, domy stają się stabilne, a jednocześnie marzenia o pokonaniu grawitacji zyskują realny kształt!
Równania trygonometryczne w codziennej nawigacji

Bardzo ważne jest także wykorzystanie równań trygonometrycznych w nawigacji – zarówno morskiej, jak i lądowej! Wyobraźcie sobie kapitana statku, pełnego żeglarskich marzeń, któremu dosłownie znika fala! Co wtedy robi? Sięga po pomoce nawigacyjne i stosuje równania trygonometryczne, aby ustalić kurs i bezpiecznie dotrzeć do portu. Dla niego zatoka wygląda jak taca wypełniona owocami morza, a poprawne obliczenia kątowe stają się kluczem do pysznego obiadu (lub przynajmniej do niezgubienia się w bezkresnych otchłaniach mórz)!
Na koniec, nie możemy zapomnieć o sportowcach, szczególnie tych zajmujących się sportami ekstremalnymi, takimi jak snowboardziści czy wspinacze. Dla nich równania trygonometryczne działają niczym osobisty GPS. Umożliwiają obliczanie kątów, prędkości oraz korzystnych trajektorii skoków. Dzięki temu potrafią nie tylko lądować na przyjemnym śniegu, ale także perfekcyjnie unikać przeszkód, co sprawia, że każdy zjazd to czysta radość! W ten sposób trygonometria nie tylko ułatwia życie, ale również czyni je bardziej ekscytującym!
Najczęstsze pułapki w rozwiązywaniu równań trygonometrycznych i jak ich unikać
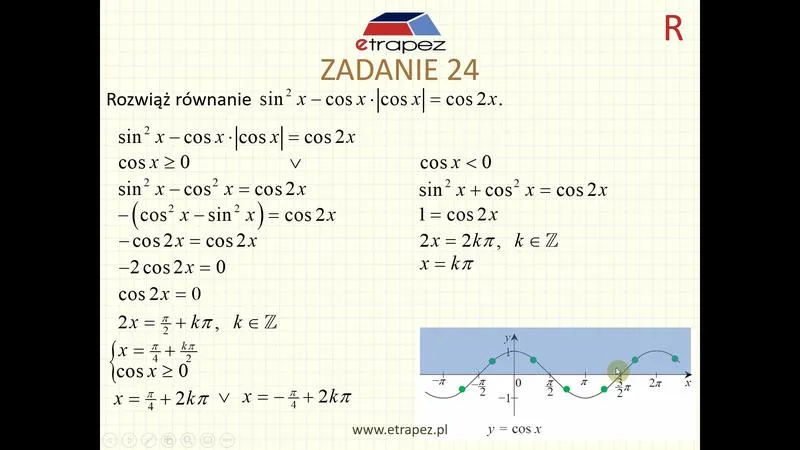
Rozwiązywanie równań trygonometrycznych to fascynująca zabawa, aczkolwiek pełna pułapek, które mogą zaskoczyć nieuważnych uczniów. Na przykład, zbyt wczesne zniechęcenie do tematu stanowi jedną z najczęstszych pułapek. Przykład? Rozwiązując równanie \( \sin x = a \), zapominamy, że rozwiązania istnieją jedynie wtedy, gdy \( a \) znajduje się w przedziale od minus jednego do jednego. Dlatego jeśli ktoś skupi się na tym równaniu bez uprzedniego sprawdzenia zakresu, jego radość po chwilowym wzlocie nadziei szybko zamieni się w przygnębienie, gdy odkryje, że znalazł się w pułapce bez wyjścia. Dlatego zapamiętaj złotą zasadę: zawsze sprawdzaj zakres!
Przechodząc do innej pułapki, warto zauważyć, że zapominanie o nieskończoności rozwiązań to powszechny błąd. Równania trygonometryczne, niczym nieproszeni goście na przyjęciu urodzinowym, często przynoszą ze sobą dodatkowe rozwiązania. Kiedy uda nam się znaleźć jedno rozwiązanie, np. \( x_0 \), musimy wiedzieć, że do niego dołączają jeszcze serie rozwiązań w postaci \( x = x_0 + k \cdot 2\pi \) oraz \( x = \pi - x_0 + k \cdot 2\pi \). Dlatego, gdy już zaczynasz wyłowić rozwiązania, pamiętaj, by rozszerzać to grono, aby nikt nie czuł się osamotniony w swoim równaniu.
Jak uniknąć typowych błędów?
Następną pułapką, na którą warto zwrócić uwagę, jest ignorowanie dziedzin funkcji trygonometrycznych. Na przykład, przy tangensie napotykamy ograniczenia, które wykluczają \( x = \frac{\pi}{2} + k\pi \). Gdy zapomnimy o tych ograniczeniach, nasze równanie może zakończyć się tragicznie, niczym film bez happy endu! Dlatego zawsze, przy każdym przekształceniu pamiętaj o zakazanych miejscach, a błędy będą cię omijały szerokim łukiem.
Ostatnią, lecz nie mniej istotną pułapką, jest brak cierpliwości. Często, po długim rozwiązywaniu, gdy nie widzimy rezultatu, mamy ochotę wszystko rzucić w kąt. Jednak miarą sukcesu nie jest tylko znalezienie rozwiązania, ale również zrozumienie całego procesu! Najlepiej podejść do problemu jak do wyzwania w grze – nawet jeśli nie wygrasz za pierwszym razem, pamiętaj, że praktyka czyni mistrza!
- Zbyt wczesne zniechęcenie do tematu - pamiętaj, żeby nie rezygnować z powodu trudności.
- Zapominanie o nieskończoności rozwiązań - zawsze uwzględniaj dodatkowe rozwiązania w równaniach trygonometrycznych.
- Ignorowanie dziedzin funkcji trygonometrycznych - zwracaj uwagę na ograniczenia, takie jak wykluczenie tangensa.
- Brak cierpliwości - nie poddawaj się przy pierwszych trudnościach, praktyka czyni mistrza.
| Pułapka | Opis |
|---|---|
| Zbyt wczesne zniechęcenie do tematu | Pamiętaj, żeby nie rezygnować z powodu trudności. Sprawdzaj zakres przed rozwiązaniem. |
| Zapominanie o nieskończoności rozwiązań | Zawsze uwzględniaj dodatkowe rozwiązania w równaniach trygonometrycznych. |
| Ignorowanie dziedzin funkcji trygonometrycznych | Zwracaj uwagę na ograniczenia, takie jak wykluczenie tangensa. |
| Brak cierpliwości | Nie poddawaj się przy pierwszych trudnościach, praktyka czyni mistrza. |
Pytania i odpowiedzi
Jakie podstawowe funkcje trygonometryczne są kluczowe w rozwiązywaniu równań trygonometrycznych?
Podstawowe funkcje trygonometryczne, które są kluczowe w rozwiązywaniu równań trygonometrycznych, to sinus, cosinus oraz tangens. Każda z nich posiada unikalne zdolności, które ułatwiają analizę i rozwiązanie równań w tym zakresie.
Czy wszystkie wartości \( a \) w równaniach trygonometrycznych są dopuszczalne?
Nie, w równaniach trygonometrycznych wartość \( a \) musi mieścić się w określonych granicach. Dla funkcji sinus i cosinus musi wynosić od -1 do 1, w przeciwnym razie rozwiązania nie będą istniały.
Jakie jest znaczenie rysowania wykresów przy rozwiązywaniu równań trygonometrycznych?
Rysowanie wykresów jest istotne, ponieważ pozwala na wizualizację punktów przecięcia funkcji, które odpowiadają rozwiązaniom równań. Analiza wykresów funkcji sinus, cosinus czy tangens oraz linii stałych pozwala łatwo zidentyfikować wartości kątów, które są rozwiązaniami.
Jakie pułapki należy unikać podczas rozwiązywania równań trygonometrycznych?
Należy unikać kilku pułapek, takich jak zbyt wczesne zniechęcenie się, zapominanie o nieskończoności rozwiązań, ignorowanie dziedzin funkcji trygonometrycznych oraz braku cierpliwości. Każda z tych pułapek może prowadzić do błędnych wyników lub frustracji, dlatego warto być czujnym na te aspekty.
Jakie są praktyczne zastosowania równań trygonometrycznych w codziennym życiu?
Równania trygonometryczne mają wiele praktycznych zastosowań, na przykład w budownictwie, astronomii czy nawigacji. Używane są do obliczeń kątów, wysokości oraz odległości, co pomaga w projektowaniu struktur, nawigacji statków czy odczytywaniu pozycji gwiazd.