Wartość bezwzględna działa jak matematyczny superbohater, zawsze stawiając na prostotę i jasność! Wyobraź sobie długi odcinek drogi, na którym każda liczba reprezentuje inny punkt na trasie. Wartość bezwzględna odpowiada na pytanie: „Jak daleko jesteś od zera?” Przy tym ignoruje, czy stoisz po lewej, czy po prawej stronie. Dzięki temu, zamiast skupiać się na nieprzyjemnych ujemnych wartościach, przekształca je w przyjazne i zrozumiałe liczby dodatnie. Zdefiniowana jako |x|, spełnia proste zasady: jeśli x jest większe lub równe zero, to |x| = x, a jeżeli jest mniejsze, to |x| = -x. Proste, prawda?
Przechodząc teraz do ważnej kwestii, zastanówmy się, co sprawia, że wartość bezwzględna odgrywa kluczową rolę w różnych dziedzinach. Na przykład w fizyce, kiedy dyskutujemy o odległości, nie interesuje nas, czy przeszliśmy 5 metrów w prawo (co zapisujemy jako +5), czy w lewo (-5). Właśnie tutaj wartość bezwzględna pokazuje, że w obydwu przypadkach odległość wynosi 5. Oznacza to, że w rozmaitych dziedzinach – od inżynierii po finanse – wartość bezwzględna pełni rolę uniwersalnego miernika, zajmując się jedynie rozmiarem bez konieczności przejmowania się kierunkami!
Praktyczne zastosowania wartości bezwzględnej
Spójrz na to, jak często korzystamy z wartości bezwzględnej w codziennym życiu. Na przykład, kiedy dowiadujesz się, że cena jakiegoś produktu wzrosła o 10 zł, nie martwisz się, czy wcześniej spadła o 10 zł. Interesuje Cię jedynie fakt, że zmiana wynosi 10 zł, niezależnie od kierunku. Nawet w gotowaniu, rozważając ilość składników, każde odstępstwo od przepisu nie stanowi dramatu; według wartości bezwzględnej, istotna pozostaje jego wielkość, a nie kierunek – czyli w górę czy w dół. Dlatego wartość bezwzględna nie tylko wspiera nas w matematyce, ale także ułatwia podejmowanie codziennych decyzji!
Na koniec warto zauważyć, że choć wartość bezwzględna może wydawać się prostym pojęciem, jej bardziej zaawansowane zastosowania w równaniach i nierównościach sprawiają, że jej rola jest nieoceniona. Niezależnie od tego, czy rozbijasz równanie na przypadki, czy analizujesz różnice w danych, wartość bezwzględna zawsze wnosi coś istotnego. Matematyczni odkrywcy powinni zatem dobrze opanować tę umiejętność – bo w końcu każdy matematyk powinien stać się „wartościowcem bezwzględnym”!
Zastosowania modułu w codziennym życiu: od finansów po inżynierię
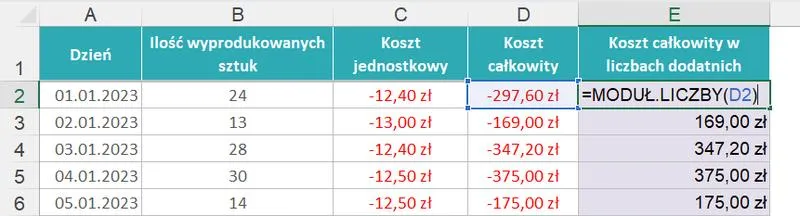
Moduł, którego możesz znać jako wartość bezwzględną, to matematyczne pojęcie, które potrafi zaskoczyć swoją wszechstronnością. Jak to działa? Otóż moduł informuje nas, jak daleko liczba znajduje się od zera na osi liczbowej, niezależnie od tego, czy jest dodatnia, czy ujemna. Mówiąc wprost, to tak, jakbyśmy spojrzeli na swoją wagę.
Przenieśmy się do fascynującego duetu – modułu i finansów! Każdy, kto miał na swoim koncie inwestycje, doskonale rozumie, jak kluczowa jest analiza ryzyka. Dzięki wartości bezwzględnej inwestorzy zyskują możliwość szybkiej oceny, jak bardzo ich portfel zyskał lub stracił, ignorując przy tym kierunek tej zmiany.
Zastosowania modułu w inżynierii
Przechodzimy teraz do magicznego świata inżynierii! Tutaj moduł staje się niezastąpionym towarzyszem inżynierów, którzy projektują mosty, budynki oraz inne konstrukcje. Wartość bezwzględna pełni istotną rolę w mierzeniu tolerancji wymiarowych, a robi to w naprawdę efektywny sposób! Wyobraź sobie, że inżynierowie przewidują długość krawędzi mostu na 5 metrów.
Oto kilka zastosowań wartości bezwzględnej w inżynierii:
- Obliczanie tolerancji wymiarowej
- Analiza odległości między strukturami
- Ocena stabilności budowli
Moduł wkracza również do codziennego życia niczym superbohater, gotowy na weekendowe plany! Obliczając odległość między dwoma punktami – na przykład korzystając z GPS – wartość bezwzględna pozwala na uzyskanie wielkości odległości, niezależnie od kierunku, w którym zmierzysz. A w sporcie, różnica punktów między drużynami zawsze przyjmuje wartość dodatnią – w końcu żaden kibic nie pragnie usłyszeć, że ich drużyna wygrała, ale dopiero po uwzględnieniu „minusów”. Tak oto, moduł sprawia, że życie staje się łatwiejsze, przyjemniejsze i… nieco bardziej uporządkowane!
Wartość bezwzględna w analizie funkcji: jak wpływa na interpretację wykresów
Wartość bezwzględna, mimo że na pierwszy rzut oka wydaje się prosta jak bułka z masłem, ma na celu ułatwienie nam analizy funkcji i zrozumienia wykresów. Wyobraź sobie, że spacerujesz po pięknej, płaskiej osi liczbowej. W pewnym momencie napotykasz liczby ujemne, a dla większości ludzi oznaczają one kłopoty. Kiedy jednak mówimy o wartości bezwzględnej, wszystkie liczby zmieniają się w grzeczne i przyjmują swoją "pozytywną" formę. To jak czarowanie, które sprawia, że każda liczba krzyczy: "Hej, patrzcie, jestem dodatnia!"
Intrygujące jest to, że w kontekście wykresów wartości bezwzględne pomagają wyodrębnić odległość od zera. Jeśli posiadasz wykres funkcji, która trzyma się dodatnich wartości, to gdy dotknie zera, wartość bezwzględna kieruje ją w stronę dodatnią. Niech to ponownie wywoła uśmiech! Na przykład w przypadku funkcji \(y = |x|\) każda wartość ujemna przekształca się w dodatnią, tworząc piękny kształt litery "V". Wygląda tak, jakbyśmy wychodzili na zewnątrz przy tradycyjnej krawędzi latarni.
Dlaczego wartość bezwzględna ma znaczenie?

Omawiając różne aspekty, dostrzegamy, że wartość bezwzględna odgrywa kluczową rolę w głębszych analizach matematycznych. Czy kiedykolwiek zajmowałeś się badaniem różnic pomiędzy liczbami? Na przykład, pytanie "jak bardzo różnią się te dwie liczby?" przekształca się w bardziej fachowe "jaka jest wartość bezwzględna różnicy tych dwóch liczb?" Dzięki temu odejmowanie staje się łatwiejsze, a obliczanie odległości pomiędzy dwoma punktami na osi to już prosta sprawa! Hura dla wartości bezwzględnej, która uratowała nas przed chaosem!
Oczywiście, nie można zapomnieć o rezultatach, które otwierają stare drzwi dla studentów zmagających się ze zrozumieniem pojęć równań oraz nierówności związanych z wartością bezwzględną. Równania i nierówności przestają być zagadkami, a stają się przyjemnymi wyzwaniami do rozwiązywania, gdy rozkładamy problem na części pierwsze. W ten sposób wartości bezwzględne działają jak magiczne miarki, które kontrolują to, co znajduje się "około" zera, a co "wykracza" poza jego granice. Mądrze analizując funkcje, możemy odkrywać fascynujący świat matematyki bez zbędnych komplikacji! W końcu, kto nie chciałby, aby liczby były po naszej stronie?
Moduł w matematyce wyższej: zrozumienie i jego rola w teorii liczb
Moduł stanowi jednego z tych matematycznych bohaterów, którzy nieustannie potrafią zaskakiwać. Przypomina on informatora z lat osiemdziesiątych w kafeterii, który wygłasza swoje myśli, a następnie zjawia się nagle na horyzoncie. W matematyce wyższej, klasyczna definicja modułu jako wartości bezwzględnej opiera się na prostym wzorze, przypominającym przepis na udane ciasto: "zrób to, a otrzymasz ciasto". W związku z tym, dla liczby x mamy |x|, a dodatnie argumenty zachowują się jak grzeczne dzieci, które dostają to, czego pragną, podczas gdy ujemne stają się ich przeciwieństwami, lecz z uśmiechem na twarzy. Jak mawiał Einstein: "Wszystko jest względne, oprócz modułu!"
Moduł i Jego Magiczne Właściwości
Nie sposób ukryć, że moduł dysponuje znacznie większą liczbą właściwości niż przeciętny superbohater. Przede wszystkim, zawsze pozostaje większy lub równy zeru, co sprawia, że czujesz się z nim jak w bezpiecznej przystani, ponieważ |x| nigdy nie zapadnie się w dół. Co ważne, |x| jest równy |-x| – ta symetria sugeruje, że moduł ma w sobie coś z wróżki. W każdym razie, jego obecność w teorii liczb to jedynie jedno z wielu zastosowań – możemy porównać go do małego ogrodnika, ale z ogromnym sercem w powieści o liczbach.
Rola Modułu w Teorii Liczb
Przyjrzyjmy się teraz, jak moduł odnajduje swoje miejsce w teorii liczb. Wyobraź sobie, że jesteś starożytnym matematykiem, a każda liczba stanowi bezpieczne schronienie. Moduł ułatwia zrozumienie różnic między tymi schronieniami. Dzięki niemu potrafimy rozwiązywać równania i nierówności w bardziej przystępny sposób. Analizując równanie |x-3| < 5, odkrywamy, że x znajduje się w pewnym przedziale, a to właśnie moduł wskazuje, jak daleko nasze liczby oddalone są od swoich "domów". Moduł jest niczym dowcipniś, który zna wszystkie tajemnice liczbowego królestwa!
Co więcej, moduł znajduje szerokie zastosowanie w wielu dziedzinach, od statystyki po inżynierię, dostarczając nam narzędzi do analizy danych, mierzenia wystających błędów oraz przewidywania niespodzianek. Trudno wyobrazić sobie matematykę bez modułu – to jak pizza bez sera, niby jest, ale czy to naprawdę to samo? Dzięki temu małemu, jednak niezwykle istotnemu pojęciu, nasza liczbowo-matematyczna podróż staje się znacznie łatwiejsza oraz przyjemniejsza. Czego chcieć więcej?
- Moduł zachowuje się jak wartość bezwzględna, zawsze większa lub równa zeru.
- Moduł jest symetryczny: |x|=|-x|.
- Moduł pomaga w zrozumieniu różnic między liczbowymi "schronieniami".
- Moduł ułatwia rozwiązywanie równań i nierówności.
- Moduł znajduje zastosowanie w wielu dziedzinach, takich jak statystyka i inżynieria.
Powyższa lista przedstawia kluczowe właściwości modułu oraz jego miejsca w matematyce i zastosowaniach praktycznych.
| Właściwość | Opis |
|---|---|
| Wartość bezwzględna | Moduł zawsze jest większy lub równy zeru. |
| Symetria | Moduł jest równy |-x|, co sugeruje jego symetryczność. |
| Zrozumienie różnic | Moduł pomaga zrozumieć różnice między liczbowymi "schronieniami". |
| Rozwiązywanie równań | Ułatwia rozwiązywanie równań i nierówności. |
| Zastosowanie | Moduł znajduje szerokie zastosowanie w statystyce, inżynierii i innych dziedzinach. |