Bezproblemowe obliczanie wysokości w trójkącie prostokątnym – sprawdzone metody i wskazówki

Obliczanie wysokości w trójkącie prostokątnym przypomina łatwe jak bułka z masłem zadanie. Mimo to, wiele osób czuje lęk na samą myśl o geometrii. Zaczynamy od podstaw, a więc od definicji wysokości. Wysokość trójkąta to najkrótszy odcinek, który łączy wierzchołek z przeciwnym bokiem, tak tworząc kąt prosty. Innymi słowy, to ta linijka, która ma za zadanie “złapać” naszą figurę w elegancki sposób, a jednocześnie zapewnić, że wszystko będzie prosto i schludnie. W trójkącie prostokątnym wysokości stanowią dwie przyprostokątne, co czyni je sojusznikami w tej matematycznej układance!

Jak obliczyć wysokość w trójkącie prostokątnym?

Przechodzimy teraz do sedna sprawy – jak obliczyć tę wysokość? W przypadku trójkąta prostokątnego mamy do dyspozycji kilka prostych wzorów. Najbardziej popularny to h = (a * b) / c, gdzie a i b oznaczają długości przyprostokątnych, a c to przeciwprostokątna. Ten wzór to klasyczne przekształcenie wzoru na pole trójkąta. Po co więc męczyć się z wynikami, które mogłyby obciążyć umysł, skoro istnieje prostsza droga? Znać długości boków to jedno, jednak uchwycenie wysokości to prawdziwa sztuka! Oczywiście, przy korzystaniu z tego wzoru musisz mieć na uwadze, na jaki bok opadasz swoją matematyczną strzałę.

Dlaczego wysokości mają znaczenie?

Wysokość w trójkącie prostokątnym nie jest jedynie pustą linią – pełni wiele istotnych ról! Stanowi kluczowy element w obliczeniach pól, a także znajduje zastosowanie w różnych zadaniach matematycznych i inżynieryjnych. Ortocentrum, czyli punkt, w którym zbiegają się wysokości trójkąta prostokątnego, znajduje się bezpośrednio w wierzchołku kąta prostego. To niezwykły fakt, który ukazuje, jak geometryczne elementy łączą się ze sobą. Nie bójcie się – wasze umiejętności matematyczne wzrosną o kilka centymetrów, o ile tylko zadbacie o te wszystkie wysokości podczas obliczeń!

Podsumowując, obliczanie wysokości w trójkącie prostokątnym nie jest żadną filozofią. Wystarczy znać kilka podstawowych wzorów, a także zrozumieć, co dzieje się, gdy mówimy o tej linii łączącej wierzchołek z podstawą. Przypominajcie sobie o przyprostokątnych jako o waszych przyjaciołach w tej matematycznej podróży, a z pewnością wyjdziecie z tego z podniesioną głową!

Zastosowanie wzorów matematycznych w praktyce

Matematyka przypomina magiczny świat, w którym zamiast czarodziejskich różdżek posługujemy się wzorami. Te wzory otwierają przed nami drzwi, które prowadzą do odkrywania wielu tajemnic otaczającej nas rzeczywistości. Na pierwszy rzut oka liczby i symbole mogą budzić w nas wątpliwości, jednak z czasem zaczynamy dostrzegać ich fascynujące zastosowanie w codziennym życiu. Bez względu na to, czy pracujemy w kuchni, budujemy dom, czy podejmujemy się bardziej złożonych obliczeń, matematyka czai się na każdym kroku, gotowa by pomóc nam w rozwiązywaniu niejednej zagadki. Oprócz ułatwiania nam życia, wzory matematyczne sprawiają, że każdy dzień staje się znacznie bardziej interesujący!

Wzory matematyczne w codziennych sytuacjach

Wyobraźmy sobie sytuację, w której pieczesz ciasto. Może nawet wyjątkowy tort urodzinowy dla babci, która już nie może się doczekać, by go skosztować. W takim przypadku musisz dokładnie obliczyć powierzchnię blachy, aby upewnić się, że ciasto wypełni ją w całości. Do tego wystarczy użyć prostego wzoru na pole prostokąta: długość razy szerokość. To naprawdę proste, prawda? Gdybyś nie opanował takich matematycznych umiejętności, Twoje kulinarne eksperymenty mogłyby skończyć się rozczarowaniem, zamiast wywołać uśmiech na twarzy babci.

Matematyka w inżynierii i architekturze

W obszarze inżynierii oraz architektury wzory matematyczne pełnią rolę superbohaterów. Co więcej, mają swoje ulubione „zbroje” – takie jak wzór Pitagorasa oraz różne formuły do obliczeń objętości i powierzchni. Stosowanie geometrii w budownictwie umożliwia projektowanie stabilnych konstrukcji, które na pewno nie zawiodą nas przy pierwszym podmuchu wiatru. Dzięki tym wzorom inżynierowie mają możliwość precyzyjnego obliczenia wysokości, kątów oraz innych kluczowych parametrów, dzięki czemu każdy budynek, most czy wiatrak może stać dumnie w przestrzeni. W przeciwnym razie, bez tego matematycznego wsparcia, wszystko mogłoby kończyć się krzywymi budowlami i zgubnymi inwestycjami.

Oto kilka kluczowych wzorów i formuł matematycznych, które są używane w inżynierii i architekturze:

Wzór Pitagorasa: a² + b² = c²
Wzór na pole prostokąta: P = długość × szerokość
Wzór na objętość prostopadłościanu: V = długość × szerokość × wysokość
Wzór na pole trójkąta: P = (podstawa × wysokość) / 2
Wzór na objętość walca: V = π × r² × h

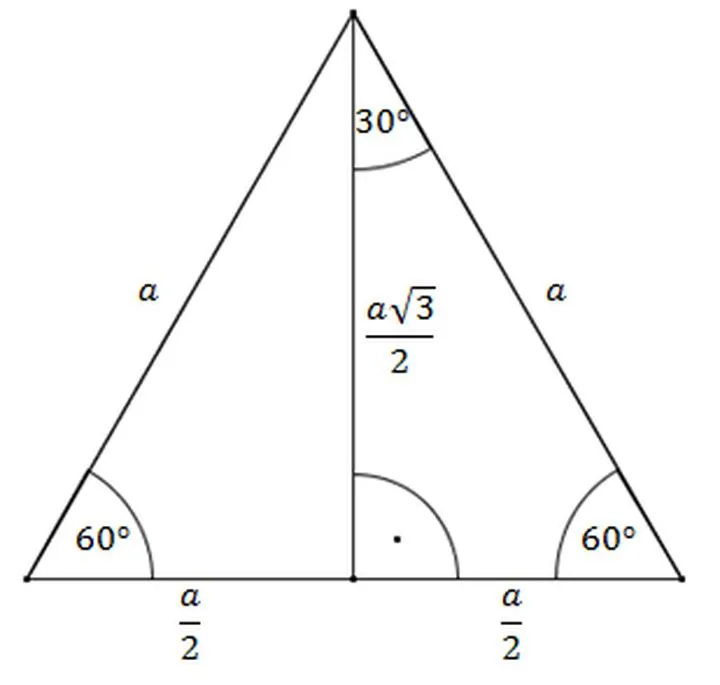
Ostatnio nauka matematyki oraz wzorów w szkole sprawia, że odkrywamy w sobie kreatywne myślenie. To zmusza nas do poszukiwania rozwiązań, wnikliwej analizy danych, a niekiedy nawet wymaga umiejętności rozwiązywania zagadek. Zamiast postrzegać wzory jako dość nudną tabelę w matematycznej przestrzeni, warto zacząć traktować je jako narzędzia – klucze do odkrywania niezwykłych aspektów naszego życia. Matematyka to nie tylko zbiór zasady, ale także prawdziwa przygoda, która prowadzi nas przez różnorodne obszary, od kuchni poprzez architekturę aż po odległe zakątki wszechświata! Co więcej, nigdy nie wiadomo, kiedy na tej drodze odkryjesz coś niezwykłego. Może nawet zdobędziesz tytuł mistrza kuchni lub projektanta dróg!

Czy wiesz, że wiele nowoczesnych technologii, takich jak systemy GPS, opiera się na wzorach matematycznych związanych z geometrią, w tym na zasadzie Pitagorasa? Dzięki nim możemy precyzyjnie obliczać odległości i lokalizacje, co umożliwia nam nawigację z niespotykaną wcześniej dokładnością!

Najczęstsze błędy przy obliczaniu wysokości trójkątów prostokątnych

Obliczanie wysokości trójkątów prostokątnych wydaje się być dość prostą sprawą. Jednak bardzo łatwo można wpaść w pułapki matematycznego myślenia. Zaczynając od podstaw, każdy trójkąt prostokątny ma znakomicie zdefiniowaną wysokość. Ta wysokość to odcinek opuszczony z wierzchołka kąta prostego na przeciwprostokątną. W tym momencie pojawiają się trudności, ponieważ wiele osób myśli, że wystarczy tylko zmierzyć odpowiednie boki, a reszta jakoś się ułoży. Nic bardziej mylnego! Nieodpowiedni wybór podstawy, na którą opadną nasze wysokości, potrafi prowadzić nas na manowce obliczeń.

Wielu wydaje się, że najłatwiejszym sposobem na obliczenie wysokości jest zastosowanie prostego wzoru. Jeśli natomiast znasz długości przyprostokątnych, to masz zadanie ułatwione, ponieważ możesz skorzystać z formuły \( h = \frac{(a \cdot b)}{c} \). Niemniej jednak, nie wolno zapominać o istotnych detalach! Przed przystąpieniem do obliczeń warto upewnić się, że dobrze zdefiniowaliśmy, która z wysokości nas interesuje. Kiedy znajdziesz się w wirze obliczeń, łatwo zapomnieć o różnych wysokościach oraz ich właściwościach, co na pewno nie sprzyja sukcesowi.

Jakie są najczęstsze pomyłki?

Jednym z częstszych błędów pojawiających się przy obliczaniu wysokości trójkąta prostokątnego jest mylenie wysokości, którą należy obliczyć. Warto pamiętać, że w przypadku wysokości opuszczonej na przeciwprostokątną, należy sięgnąć po zupełnie inny wzór. Jeśli jednak wybierzemy przyporządkowane, nasze obliczenia staną się dość chaotyczne. Dodatkowo, niektórzy uczniowie zbyt szybko przeskakują do korzystania z gotowych wzorów, nie doszli do właściwego zrozumienia materiału – a to jest pierwszy krok do katastrofy w zadaniach.

Ostatecznie kluczem do sukcesu w obliczaniu wysokości trójkątów prostokątnych pozostają cierpliwość oraz staranność. Porządkując swoje przemyślenia, przypomnij sobie podstawowe zasady, a matematyka przestanie być twoim wrogiem. Jeśli zaś zechcesz zrozumieć, co twoje obliczenia naprawdę oznaczają, wystarczy, że spojrzysz na wyniki – prawidłowe wysokości potrafią wyczarować przed tobą nie tylko znacznie łatwiejsze życie, ale także piękne kształty w sztuce geometrycznej. Czego chcieć więcej?

Błąd	Opis
Mylenie wysokości	Nieodpowiedni wybór wysokości do obliczeń, co prowadzi do błędnych rezultatów.
Nieodpowiedni wzór	Użycie niewłaściwego wzoru do obliczenia wysokości opuszczonej na przeciwprostokątną.
Za szybkie korzystanie z wzorów	Brak zrozumienia materiału i skakanie do gotowych wzorów, co prowadzi do chaosu w obliczeniach.
Brak cierpliwości	Pochopne obliczenia i brak staranności prowadzące do błędnych wyników.

Ciekawostką jest, że wysokość opuszczona na przeciwprostokątną w trójkącie prostokątnym ma również zastosowanie w wielu praktycznych dziedzinach, takich jak architektura czy inżynieria, gdzie precyzyjne obliczenia wysokości są kluczowe dla zapewnienia stabilności i estetyki budynków.

Przykłady z życia codziennego – gdzie spotykamy trójkąty prostokątne?

Trójkąty prostokątne w geometrycznym uniwersum przyciągają uwagę jak gwiazdy! Spotykamy je niemal wszędzie: w naszych domach, na boiskach, a nawet w kuchniach. Stojąc przed półką z książkami, zauważamy, że układają się w trójkąty prostokątne. Mierząc wysokość regału oraz odległość od podłogi do jego wierzchołka, przypadkowo tworzymy niewielki kąt prosty. Taki układ nie tylko wygląda estetycznie, ale także przypomina, jak geometrię można zastosować w codziennym życiu!

W budownictwie trójkąty prostokątne odgrywają kluczową rolę! Czy kiedykolwiek zastanawialiście się, jak tworzy się proste schody? Użycie trójkątów prostokątnych sprawia, że całość staje się możliwa! Kiedy stawiamy schody, mamy jedną przyprostokątną, na którą stawiamy stopę, oraz drugą, która prowadzi nas do góry. Dzięki sprytnej kombinacji kątów prostych możemy łatwo wspinać się na wyższe poziomy. Choć wydaje się to proste, to właśnie geometria czyni nasze życie bardziej funkcjonalnym.

Trójkąty w życiu codziennym

Nie sposób zapominać o roli geometrów w sporcie! Weźmy futbol jako przykład, gdzie linie boiska świetnie ilustrują trójkąty prostokątne. Rozgrywki opierają się w dużej mierze na strategii, dlatego znajomość przestrzeni boiska pozwala wyznaczyć najlepsze pozycje do złapania piłki. Oto zagadka: gdy zawodnicy wykonują zagranie w kształcie litery "L", tak naprawdę mogą tworzyć trójkąt prostokątny. Taki układ otwiera nowe możliwości, a każdy podbramkowy kąt sprzyja szansom na celny strzał!

W codziennym życiu spotykamy trójkąty prostokątne w różnych kontekstach, takich jak:

Architektura budynków i okien
Układ schodów
Strategie w sporcie, jak futbol
Wzory i kształty w designie wnętrz

Trójkąty prostokątne mają też swoje ważne miejsce w zamówieniach architektonicznych. Myślicie o trójkątnych oknach? Czemu nie! Tego rodzaju elementy wprowadzają ciekawe i nietypowe zestawienia w designie budowli. Gdy rozważamy trójkąt prostokątny jako podstawowy kształt do budowy, zdaje się, że przypomina nam on o znaczeniu solidnych fundamentów. Każdy budynek wymaga trójkątów – one działają jak szkielet w organizmie, nadając stabilności oraz elegancji. Bez wątpienia to hit każdego projektanta!

Źródła: