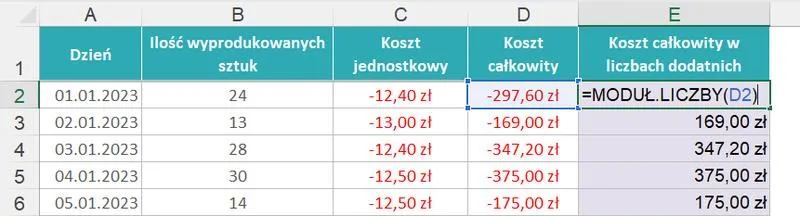
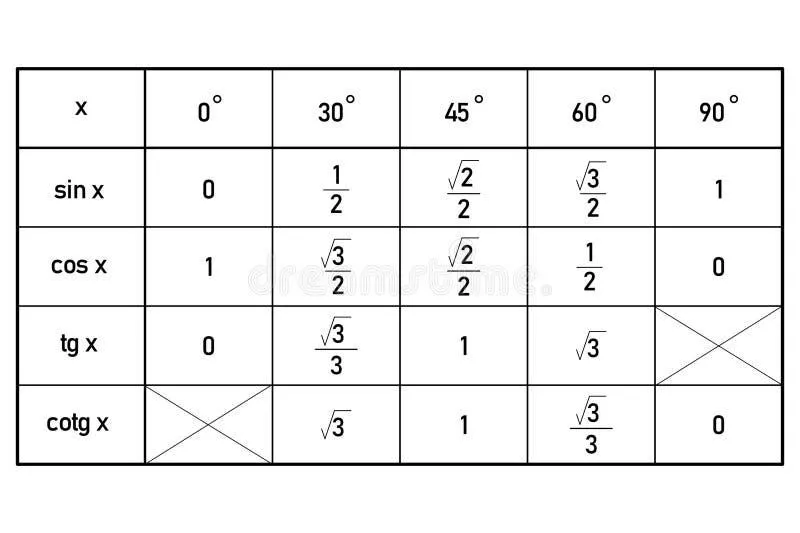
Jeśli kiedykolwiek miałeś do czynienia z trygonometrią, to z pewnością spotkałeś się z tajemniczym przyjacielem – tangensem. Ten nieco mniej znany kuzyn sinusa i cosinusa może wydawać się na początku przerażający, ale nie martw się! Wystarczy zrozumieć zasady. Tangens, znany również jako tg, to funkcja trygonometryczna, która opisuje stosunek długości przyprostokątnej naprzeciw kąta do przyprostokątnej przyległej. A wiesz co? Cała ta magia działa tylko w trójkącie prostokątnym, więc nie próbuj go szukać w innym kontekście, ponieważ to jak poszukiwanie igły w stogu siana! Przypomnijmy, że tangens tak naprawdę działa według wzoru \(\tan \alpha = \frac{\sin \alpha}{\cos \alpha}\), więc zawsze możesz go obliczyć, znając inne funkcje trygonometryczne. Uff, prościej być nie może!
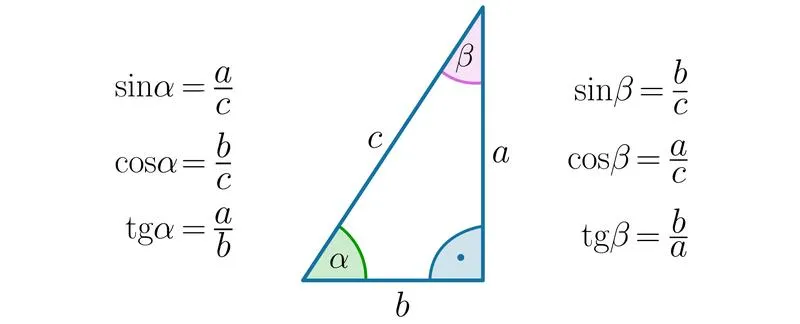
- Definicja tangensa: funkcja trygonometryczna opisująca stosunek długości przyprostokątnej naprzeciw kąta do przyprostokątnej przyległej w trójkącie prostokątnym.
- Wzór tangensa: \(\tan \alpha = \frac{\sin \alpha}{\cos \alpha}\).
- Zastosowanie tangensa: inżynieria, architektura, gry komputerowe, obliczanie kątów nachylenia.
- Znaczenie tangensa w matematyce: kluczowa rola w klasycznych wzorach trygonometrycznych.
- Kroki do obliczania kątów na kalkulatorze: sprawdzenie funkcji, ustawienie jednostek, wprowadzenie danych, wybór funkcji, dokładność w danych.
- Typowe błędy w obliczeniach: mylenie długości boków, błędne jednostki miary.
- Praktyczne zastosowania kątów: budownictwo, geodezja, nawigacja.
Niektórzy mogą myśleć, że tangens to tylko król matematyki, ale to nieprawda! To wspaniałe narzędzie zdobyło uznanie nie tylko w podręcznikach szkolnych, lecz również w inżynierii, architekturze oraz grach komputerowych! Wyobraź sobie, że stoisz na stromej górze, starając się określić kąt nachylenia. Dzięki tangensowi masz szansę stać się ekspertem w obliczaniu kątów – od schodów po dachy. W końcu kto nie chciałby wiedzieć, jak stromo nachylona jest jego nowa połacia dachowa? Jeśli znasz wysokość i długość podstawy, Twoje problemy z tangensem znikają niczym magnes!
Dlaczego tangens ma ogromne znaczenie?
Warto pamiętać, że tangens nie istnieje w próżni! Oprócz tego, że jest przydatnym narzędziem w codziennym życiu, odgrywa również kluczową rolę w klasycznych wzorach trygonometrycznych. Dzięki jedynce trygonometrycznej, którą znają wszyscy studenci (a przynajmniej powinni!), możemy posługiwać się relacją \(\sin^{2} \alpha + \cos^{2} \alpha = 1\). A wiesz co? Tangens ożywia tę równość, ukazując swoim towarzyszom, jak fundamentalne jest właściwe zrozumienie zjawisk zachodzących w trójkącie. Bez solidnego przyswojenia tangensa, łatwo można zaplątać się w gąszczu niejasnych obliczeń oraz niepotrzebnych frustracji!
Widzicie, zrozumienie tangensa to jak ekscytująca przygoda w świecie trygonometrii – pełna emocji, możliwości oraz praktycznych zastosowań! A hej, kto by pomyślał, że te wszystkie skomplikowane obliczenia mogą być po prostu narzędziami do rozwiązywania codziennych problemów? Dlatego następnym razem, gdy staniecie przed wyzwaniem obliczenia kąta, pamiętajcie o swoim najlepszym przyjacielu – tangensie. Bez niego Wasze obliczenia mogą stać się nieco bardziej skomplikowane, a życie – zdecydowanie mniej interesujące!
| Tema | Opis |
|---|---|
| Definicja Tangensa | Tangens (tg) to funkcja trygonometryczna opisująca stosunek długości przyprostokątnej naprzeciw kąta do przyprostokątnej przyległej w trójkącie prostokątnym. |
| Wzór Tangensa | \(\tan \alpha = \frac{\sin \alpha}{\cos \alpha}\) |
| Zastosowania Tangensa | Inżynieria, architektura, gry komputerowe, obliczanie kątów nachylenia (np. schody, dachy). |
| Znaczenie Tangensa | Odgrywa kluczową rolę w klasycznych wzorach trygonometrycznych, takich jak relacja \(\sin^{2} \alpha + \cos^{2} \alpha = 1\). |
| Rola w edukacji | Zrozumienie tangensa jest istotne dla posługiwania się trygonometrią i uniknięcia błędów w obliczeniach. |
| Wnioski | Tangens ułatwia codzienne obliczenia i sprawia, że matematyka staje się bardziej przystępna. |
Czy wiesz, że tangens ma swoje zastosowanie nie tylko w trójkątach prostokątnych? Dzięki niemu można także analizować zjawiska związane z ruchem harmonicznym, takimi jak drgania wahadła czy fale dźwiękowe!
Krok po kroku: Jak używać kalkulatora do obliczania kątów
Używanie kalkulatora do obliczania kątów stanowi naprawdę prostą czynność, o ile znasz kilka kluczowych zasad. Na początku dobrze jest upewnić się, czy masz odpowiedni kalkulator. Wybór urządzenia z funkcjami trygonometrycznymi to najlepsza decyzja! Na szczęście większość nowoczesnych kalkulatorów, zwłaszcza aplikacje, umożliwia obliczanie sinusów, cosinusów oraz tangensów, co można porównać do najlepszych przysmaków w menu restauracji. Pamiętaj, aby przed rozpoczęciem obliczeń zweryfikować, czy kalkulator ustawiony jest na stopnie, czy radiany. Można to porównać do sprawdzania daty ważności w sklepie – taka czynność może uratować Cię przed nieprzyjemną niespodzianką!
Wprowadź dane jak mistrz matematyki
Następnie przyszedł czas na przekazanie kalkulatorowi niezbędnych informacji. Wprowadź wartości kąta lub długości boków trójkąta prostokątnego, nad którym pracujesz (pamiętaj, aby nie pomylić boków przeciwnych i przylegających!). Jeśli już wiesz, co chcesz obliczyć – czy to sinus, cosinus, czy tangens – upewnij się, że wybierasz właściwą funkcję z menu (bo inaczej kalkulator może poczuć się zagubiony, tak jak Ty w sklepie z elektroniką!). Pamiętaj także o dokładnym użyciu przecinków lub kropek, aby kalkulator nie musiał się zastanawiać, co z tym zrobić.
- Sprawdź, czy kalkulator ma funkcje trygonometryczne.
- Upewnij się, że jest ustawiony na stopnie lub radiany.
- Wprowadź wartości kąta lub długości boków trójkąta.
- Wybierz odpowiednią funkcję: sinus, cosinus lub tangens.
- Dokładnie używaj przecinków lub kropek w danych.
Odczytaj wynik i bądź dumny z siebie!
Kiedy już wpiszesz wszystkie dane, naciśnij przycisk „Oblicz” i czekaj na magiczny wynik, który powinien się pojawić szybko, niczym dziesięć porcji frytek w fast foodzie – prosto na tacy! Po wykonaniu obliczeń warto spojrzeć na wyniki dla wszystkich funkcji trygonometrycznych. Kto wie, może potrzebujesz także innych wyników? Pamiętaj, aby nie stresować się, gdy cosinus wyjdzie ujemny – takie sytuacje się zdarzają, a matematyka ma swój urok, który potrafi objąć nawet najtrudniejsze wyzwania!
Na zakończenie pamiętaj, że korzystanie z kalkulatora, zarówno w szkole, jak i w pracy, odgrywa kluczową rolę w podejmowaniu trafnych decyzji. Dzięki temu narzędziu możesz tworzyć plany, rozwiązywać problemy matematyczne, a nawet projektować budowlane cuda. Wspaniałe, prawda? Teraz, kiedy już znasz tę sztuczkę, pora zabrać się do działania i pokazać światu, co potrafisz osiągnąć z kalkulatorem w ręku!
Typowe błędy przy obliczaniu kątów z tangensa i jak ich unikać
Obliczanie kątów za pomocą tangensa to sztuka, która niejednokrotnie stawia nawet największych geniuszy matematycznych przed trudnościami. W procesie tym można popełnić typowe błędy, które dotyczą nie tylko uczniów, ale również osób z większym doświadczeniem w matematyce. Najczęściej ludzie mylą przyprostokątne z przeciwną stroną kąta. Zapominają, która z tych długich linii jest właściwa, co prowadzi do uzyskania tangensa zupełnie innego kąta. Warto zauważyć, że można spędzić godziny na analizowaniu obliczeń, a rozwiązanie może znajdować się zaledwie na wyciągnięcie ręki.
Inną kwestią, którą warto poruszyć, są jednostki miary. Radiany czy stopnie? Ta pomyłka zdarza się najczęściej, a od niej nie sposób uciec. Wyobraź sobie sytuację, w której wprowadzasz do kalkulatora „30” i nagle zaczyna się magiczny proces – tylko że Twoje urządzenie ustawione jest na radiany. Oczekujesz pięknego wyniku, a otrzymujesz zaskakujący efekt. Staraj się unikać takich sytuacji – zawsze upewniaj się, że system, z którego korzystasz, ma właściwą jednostkę miary. Może to przynieść ulgę, gdy zamiast skomplikowanego kąta rozwiążesz problem w prostszy sposób.
Przygotowanie do Obliczeń
Aby zminimalizować błędy, warto przed każdym obliczeniem przeprowadzić mały rytuał – narysować trójkąt i oznaczyć jego boki. Przyzwyczajenie do wizualizacji problemów znacznie redukuje ryzyko popełnienia błędu. Zawsze sprawdzaj, czy dobrze rozumiesz, gdzie znajduje się przeciwprostokątna, a gdzie przyprostokątne. Po dokładnym zbadaniu swojej „architektury” zyskasz pełniejszy obraz tego, czego potrzebujesz. W końcu matematyka to nie tylko suche liczby; to także sztuka przedstawienia ich w sposób zrozumiały.
Ostatecznie magia związana z korzystaniem z tangensa oraz innych funkcji trygonometrycznych polega na umiejętnym zastosowaniu ich z odpowiednim zrozumieniem. Dlatego, drogi uczniu, niech Twoje obliczenia staną się okazją do twórczości, a nie polem minowym. Omijaj pułapki błędów, a zaskoczy Cię to, jak skomplikowana materią matematyki przekształca się w coś pięknego i zrozumiałego!
Praktyczne zastosowania obliczania kątów w życiu codziennym
Obliczanie kątów, chociaż na pierwszy rzut oka może wydawać się tematem czysto akademickim, w rzeczywistości prowadzi do wielu przydatnych rozwiązań w naszym codziennym życiu. Czy kiedykolwiek próbowałeś ustawić półkę na ścianie? Bez odpowiednich obliczeń kątów, ryzykujesz, że twoje dzieło będzie wyglądać niesymetrycznie... a może tylko na zdjęciach na Instagramie! Kiedyś, planując „kreatywną” wystawkę z książek, wyobrażałem sobie coś zupełnie innego. Jak się jednak okazało, rzeczywistość znacznie odbiegała od mojej wizji. Właśnie wtedy zapragnąłem zgłębić sekrety trygonometrii, by nigdy więcej nie ułatwiać sobie życia w dekoracyjnych wyzwaniach.
Podstawowe zastosowania w budownictwie
Nie tylko w domowym zaciszu warto znać kąt prosty. W zawodach takich jak budownictwo czy architektura, obliczanie kątów stanowi codzienność. Wyobraź sobie architekta, który planuje dach w kształcie kwiatka – w moim przypadku obliczenia kąta nachylenia dachu byłyby kluczowe, aby efekt końcowy nie przypominał nowej formy sztuki współczesnej. Tangens, sinus i cosinus stają się nieocenionymi sprzymierzeńcami, a konstrukcje unoszą się majestatycznie, zamiast garbić się w chaosie geometrycznym. Co więcej, każda inna budowla, która na co dzień służy ludziom, wymaga precyzyjnych pomiarów. Warto więc pamiętać, że każdy murowany dom, każda szopka na narzędzia – wszystkie te budowle mają w sobie odrobinę matematyki!
W geodezji i nawigacji
Geodezja to kolejny obszar, w którym kąty odgrywają kluczową rolę. Odkrywcy często manipulują kątami, aby znaleźć najlepszą drogę do skarbu… albo może tylko do pobliskiego sklepu z przekąskami. Dzięki funkcjom trygonometrycznym mogą zmierzyć odległość między punktami, które w przeciwnym razie byłyby dla nas nieosiągalne, chyba że dysponujesz dynamitem i odpowiednimi kwalifikacjami! Zresztą, nawigatorzy w terenie także muszą wykazywać się umiejętnością obliczania kątów – sprzęt GPS nie załatwia wszystkiego, zwłaszcza gdy wybierasz się na pieszą wyprawę według wskazania starodawnej mapy. Gdyby tylko każdy z nas miał w kieszeni kieszonkowy kalkulator trygonometryczny!
Oto kilka zastosowań kątów, które można wykorzystać w geodezji i nawigacji:
- Obliczanie odległości między punktami z wykorzystaniem trygonometrii.
- Ustalanie właściwego kursu w nawigacji morskiej i lądowej.
- Wykorzystywanie kątów do pomiarów wysokości obiektów.
- Ocena kątów w mapowaniu terenu oraz w pracach geodezyjnych.
Obliczanie kątów nie sprowadza się jedynie do składania matematycznych wzorów, ale także do umiejętności praktycznego stosowania ich w życiu codziennym. Dlatego następnym razem, kiedy zechcesz wyjść na budowę lub po prostu ustawić coś w swoim domu, pamiętaj o swoich kątowych przyjaciołach. Może warto nawet zainwestować w jeden z przezabawnych kalkulatorów, które na zawsze zmienią twoje podejście do matematyki! Zdecydowanie dodadzą radości w odległości każdego kąta i pomogą uniknąć wszelkich krawędziowych katastrof.
Pytania i odpowiedzi
Jak oblicza się tangens w trójkącie prostokątnym?
Tangens opisuje stosunek długości przyprostokątnej naprzeciw kąta do przyprostokątnej przyległej. Wzór na tangens to \(\tan \alpha = \frac{\sin \alpha}{\cos \alpha}\), co oznacza, że możemy obliczać tangens znając sinus i cosinus kąta.
Dlaczego warto znać tangens w życiu codziennym?
Tangens ma zastosowanie w różnych dziedzinach, takich jak inżynieria, architektura czy nawet dekorowanie wnętrz. Dzięki niemu możemy dokładnie obliczać kąty nachylenia, co jest niezwykle przydatne przy budowie lub aranżacji przestrzeni.
Jakie kroki należy wykonać, korzystając z kalkulatora do obliczania kąta tangensa?
Aby obliczyć kąt tangensa, upewnij się, że kalkulator ma funkcje trygonometryczne i jest ustawiony na odpowiednie jednostki miary (stopnie lub radiany). Następnie wprowadź wartości, wybierz funkcję tangensa i naciśnij "Oblicz", aby uzyskać wynik.
Jakie są najczęstsze błędy przy obliczaniu kątów z tangensa?
Najczęstsze błędy obejmują mylenie przyprostokątnych z przeciwną stroną kąta oraz niepoprawne ustawienia jednostek (radiany zamiast stopni). Zaleca się wizualizację problemu oraz sprawdzenie jednostek przed każdą kalkulacją, aby zminimalizować ryzyko błędów.
Jakie są praktyczne zastosowania obliczania kątów w różnych dziedzinach?
Obliczanie kątów jest kluczowe w budownictwie, geodezji i nawigacji. Umożliwia precyzyjne pomiary, ustalanie kursów oraz oceny wysokości obiektów, co ma istotne znaczenie w pracy zawodowej oraz codziennych zadaniach.