Logarytmy stanowią jeden z tych elementów matematyki, które potrafią przyprawić o ból głowy, jednak jednocześnie okazują się niesamowicie przydatne! Dlaczego warto je znać? Mają moc zdziałania cudów podczas obliczeń, które na pierwszy rzut oka wyglądają jak czarna magia. Pojawiają się w różnych dziedzinach nauki, od informatyki po ekonomię, a ich znajomość znacząco ułatwia życie każdemu, kto choć raz miał do czynienia z potęgami. W końcu, wskazując na logarytm, zapraszamy do świata, w którym przekształcamy skomplikowane operacje w coś znacznie prostszego!
Bez obaw, logarytmy to nie potwory!
Przede wszystkim, logarytmy pomagają nam w obliczeniach. Zamiast żmudnie mnożyć i dzielić, wystarczy zastosować właściwe wzory logarytmiczne! Na przykład, gdy musimy obliczyć logarytm iloczynu, wystarczy przypomnieć sobie zasady i wykorzystać odpowiednie wzory. Po co męczyć się, skoro możemy uprościć rachunki? Logarytmy o wspólnej podstawie sugerują, że zamiast mnożyć dwie liczby, wystarczy dodać ich logarytmy! To prawdziwa magia, prawda?
Logarytmy na co dzień!
Niezaprzeczalnie, logarytmy przydają się również w codziennym życiu, zwłaszcza w takich dziedzinach jak finanse i nauka. Wyobraźcie sobie, że znajdujecie się w sklepie i myślicie, ile razy musicie zwiększyć swoją inwestycję, aby uzyskać zysk. A właśnie, do tego przydaje się logarytm! Dzięki niemu zrozumiecie, jakie zmiany zaszły w waszym bilansie finansowym. Logarytmy stanowią furtkę do oceny wzrostu i spadku, co w innych sytuacjach wymagałoby znacznie więcej czasu na obliczenia. Dodatkowo, posługiwanie się logarytmami podczas trudnych rozmów pozwala zyskać szacunek wśród znajomych - pamiętajcie tylko, by podzielić się swoimi tajemniczymi sztuczkami!
Podsumowując, logarytmy nie są jedynie teoretycznym konceptem, ale praktyczną umiejętnością, która przydaje się w wielu aspektach życia. Kiedy zrozumiemy, że logarytm to jedynie sposób na przekształcanie skomplikowanych działań, otworzy się przed nami nowy świat matematycznych możliwości. Każdy logarytm to nie tylko nudny symbol, ale klucz do szybkich obliczeń i efektywnego myślenia, które pozwala doskonalić nasze umiejętności analityczne w każdej dziedzinie. Warto więc zgłębić ten fascynujący świat logarytmów i czerpać z niego korzyści!
Krok po kroku: Jak obliczać logarytmy ręcznie?
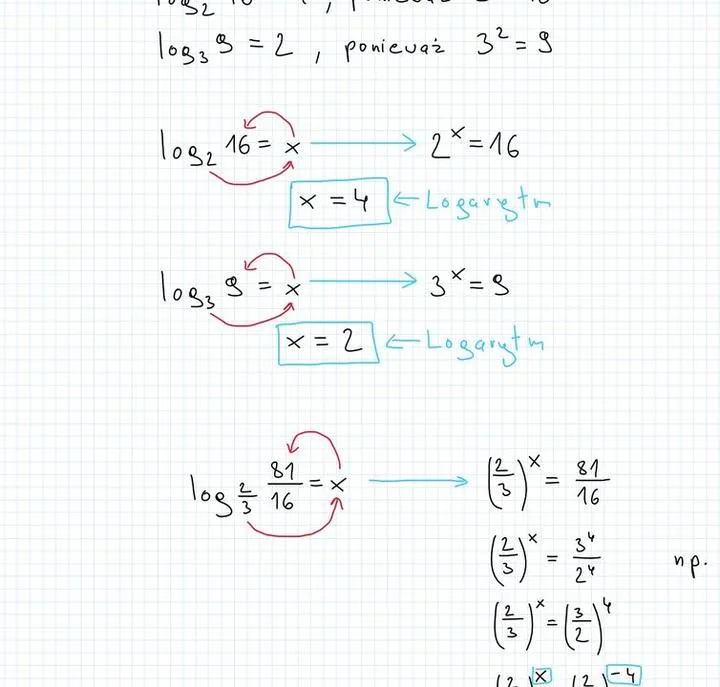
Obliczanie logarytmów ręcznie na początku może wydawać się nieco przerażające, jednak z odpowiednim podejściem przerodzi się w czystą przyjemność. Zacznijmy od przypomnienia sobie definicji logarytmu, która stwierdza, że logarytm liczby \(b\) przy podstawie \(a\) jest równy \(x\) wtedy, gdy \(a\) podniesione do potęgi \(x\) daje \(b\). Innymi słowy, mamy do czynienia z równaniem: \(a^x = b\). W takim razie rozpocznijmy naszą przygodę z logarytmicznymi potęgami, a przekonacie się, że nawet trudne zadania mogą okazać się małe jak myszka!
Pierwszy krok na drodze do logarytmicznego mistrzostwa polega na przekształceniu zapisanego logarytmu do równania potęgowego. Wystarczy zadać sobie proste pytanie: Do jakiej potęgi muszę podnieść moją podstawę logarytmu, aby uzyskać daną liczbę? Na przykład, rozważając \( \log_{2} 8 \), odpowiadamy na pytanie: „Do jakiej potęgi podnieść \(2\), aby uzyskać \(8\)?” Odpowiedzią będzie oczywiście \(3\), co oznacza, że \( \log_{2} 8 = 3\). W związku z tym, logarytmy mogą okazać się naprawdę ciekawe! Z basketem w ręku, kontynuujemy naszą podróż!
Jak sobie radzić z trudniejszymi przypadkami?
Czasami pojawią się logarytmy, które wymagają większej kreatywności. Na przykład, w przypadku napotkania \( \log_{4} \frac{1}{2} \), musimy pomyśleć, jak przekształcić ułamek na formę potęgi. Możemy zamienić \( \frac{1}{2} \) na \( 2^{-1} \). Skoro \(4\) to \(2^2\), podnosimy to do \(x\) i otrzymujemy równanie: \( (2^2)^x = 2^{-1} \). Porównując wykładniki, uzyskujemy rozwiązanie. Ragabum, logarytm rozwiązany!

Logarytmy mogą wydawać się chaotyczne, jednak z odpowiednim treningiem stają się nie tylko zrozumiałe, ale wręcz satysfakcjonujące. Poniżej przedstawiam kilka technik, które mogą pomóc w obliczaniu logarytmów:
- Użycie wzorów logarytmicznych, takich jak logarytm iloczynu i sumy.
- Przekształcanie liczb do postaci potęg, co znacznie ułatwia obliczenia.
- Wykorzystywanie kalkulatorów naukowych lub programów komputerowych do bardziej skomplikowanych operacji.
Gdy opanujecie podstawowe techniki, a liczby zaczną tańczyć na kartce papieru, zauważycie, że manualne obliczanie logarytmów przypomina grę w szachy — wymaga strategii, ale każdym razem, gdy pokonacie trudne równanie, satysfakcja będzie ogromna! Dlatego niech żyją logarytmy, a w szczególności te obliczane ręcznie! W końcu, kto powiedział, że matematyka nie może być zabawna?
Przykłady zastosowania logarytmów w różnych dziedzinach nauki
Logarytmy to matematyczne sztuczki, które z powodzeniem wykorzystujemy w różnych gałęziach nauki. Na przykład, w fizyce często analizujemy zjawiska takie jak dźwięk czy światło, a logarytmy odgrywają w tym istotną rolę. Przy obliczaniu natężenia dźwięku sięgamy po logarytm w decybelach. Zaskakujące, prawda? Nie przypuszczałem, że matematyka ma tak głośny głos. Im głośniej, tym bardziej logarytmy zmuszają nas do redukcji liczby, co z kolei rozwija nasze umiejętności obliczeniowe. Dlatego następnym razem, gdy usłyszysz „hałas”, pomyśl – to logarytmy wzywają nas na pomoc!
Logarytmy w przyrodzie
Biolodzy również chętnie korzystają z logarytmów, zwłaszcza w kontekście wzrostu populacji. Gdy rozważamy model eksponencjalny, dostrzegamy, że populacje mogą rosnąć w zawrotnym tempie. W tej sytuacji logarytmy stają się kluczowym narzędziem, które pozwala nam zrozumieć tę dynamiczną sytuację. Na przykład, w badaniach nad wzrostem komórek naukowcy korzystają z logarytmów, aby ostrzegać przed niekontrolowanym mnożeniem, ponieważ za dużo dobrego może prowadzić do problemów. Jeśli więc nie zdawaliście sobie sprawy z ich roli, teraz wiecie, że komunikat „za dużo komórek!” to w istocie... matematyczne ostrzeżenie!
Logarytmy a technologia
A co powiecie na technologię? Tutaj logarytmy pełnią rolę superbohaterów, ratując nas przed chaosem! W informatyce logarytmy mają kluczowe znaczenie w algorytmach, szczególnie tych związanych z sortowaniem i przeszukiwaniem. Gdy zbiory danych rosną w zastraszającym tempie, logarytmy ułatwiają efektywne przechowywanie i przetwarzanie informacji. Szacując czas działania algorytmu, logarytmy przychodzą z pomocą niczym Batman w Batmobilu – zawsze wtedy, gdy są najbardziej potrzebne. Dlatego pamiętajcie, następnym razem, gdy zapiszecie coś na komputerze, logarytmy będą mówiły „chap, chap, już za chwilę!”
Podsumowując nasze logarytmowe zawirowania, zauważamy, że ich zastosowanie występuje w każdej dziedzinie nauki – od fizyki przez biologię, aż po technologię. Bez logarytmów nasze zrozumienie świata przypominałoby budowanie zamku z piasku podczas sztormu – czyli chaotyczne. Dlatego nie bójmy się logarytmów, lecz odkrywajmy ich sekrety!
| Dyscyplina | Zastosowanie logarytmów | Przykład |
|---|---|---|
| Fizyka | Analiza zjawisk takich jak dźwięk czy światło | Obliczanie natężenia dźwięku w decybelach |
| Biologia | Modelowanie wzrostu populacji | Badania nad wzrostem komórek |
| Technologia | Algorytmy związane z sortowaniem i przeszukiwaniem | Efektywne przechowywanie i przetwarzanie informacji |
Ciekawostką jest to, że logarytmy nie tylko upraszczają skomplikowane obliczenia, ale również pozwalają na wizualizację danych w formie wykresów, co może być kluczowe w analizie danych w takich dziedzinach jak meteorologia, gdzie zmiany w czasie mogą być znacznie lepiej zobrazowane przy użyciu skali logarytmicznej.
Narzędzia i kalkulatory: Jak ułatwić sobie obliczenia logarytmiczne?
Kiedy myślimy o logarytmach, zazwyczaj odczuwamy pewien niepokój. Wydaje się, że te tajemnicze matematyczne symbole budzą w nas znacznie większy lęk niż nasza chęć do obliczeń. Jednak spokojnie! Różnorodne narzędzia oraz kalkulatory stoją po naszej stronie i mogą zdziałać cuda, gdy w nasze ręce wpadają logarytmiczne potoki cyfr. Kto więc powiedział, że musimy męczyć się na każdy możliwy sposób, skoro technologia doskonale nam pomaga, a co za tym idzie, ułatwia nam życie na każdym kroku? W końcu po to właśnie została stworzona!
Logarytmiczne kalkulatory - przyjaciele każdego z nas!
Jeżeli myślisz, że kalkulatory to tylko nudne, elektroniczne pudełka, czas przełamać ten mit! Dobrze dobrany kalkulator logarytmiczny działa jak nauczyciel matematyki, który zawsze jest obok, gotowy do pomocy. To narzędzie uprości obliczenia i umożliwi szybkie rozwiązanie trudnych zadań, które kiedyś mogły wydawać się nieosiągalne. Dlatego zanim spróbujesz obliczyć logarytm w pamięci, po prostu wyciągnij kalkulator. Z nim nawet logarytm \(\log_{a} b\) stanie się bułką z masłem!
Obliczenia online - bo kto nie kocha łatwego dostępu?

A co powiesz na obliczenia bez najmniejszego wysiłku? Internet to prawdziwa skarbnica narzędzi do obliczania logarytmów, które dostępne są na wyciągnięcie ręki. Wystarczy tylko kliknąć odpowiednią stronę, wpisać liczby i... gotowe! Takie programy często oferują także różne przykłady i wyjaśnienia, tak że nawet najbardziej zagubiony uczniak zdoła wyjść z tego cało jak feniks z popiołów. Dlatego zamiast kluczyć w zawirowaniach niewiedzy, sięgnij po zestaw narzędzi online i ciesz się, że matematyka stała się prostsza!
Pamiętaj, że obliczenia logarytmiczne wcale nie muszą być czasochłonne i stresujące. Dobre narzędzia działają niczym magiczne różdżki - z ich pomocą przekształcisz skomplikowane zadanie w prostą i przyjemną zabawę. W końcu, kto powiedział, że matematyka nie może być radością? Pozwól, by logarytmy zyskały nowy wymiar, a Ty czerp radość z ich odkrywania!
- Kalkulatory logarytmiczne są dostępne w różnych formach - od prostych aplikacji po bardziej zaawansowane programy.
- Wiele stron internetowych oferuje darmowe narzędzia do obliczania logarytmów.
- Obliczenia online pozwalają na szybkie uzyskanie wyników bez potrzeby manualnych obliczeń.
- Niektóre kalkulatory online oferują dodatkowe funkcje, takie jak przykłady czy wyjaśnienia teorii logarytmów.
Źródła:
- https://www.matemaks.pl/obliczanie-logarytmow.html
- https://szaloneliczby.pl/obliczanie-logarytmow/
- https://www.matemaks.pl/logarytmy.html
- https://cyrkiel.info/liceum/dzialania-na-logarytmach-2/
- https://zpe.gov.pl/a/dzialania-na-logarytmach-przyklady/D1HkdfKUz
Pytania i odpowiedzi
Jakie są podstawowe zasady obliczania logarytmów?
Podstawowe zasady obliczania logarytmów zakładają przekształcenie zapisanego logarytmu do równania potęgowego. Na przykład, aby obliczyć \( \log_{2} 8 \), należy odpowiedzieć na pytanie, do jakiej potęgi musimy podnieść \(2\), aby uzyskać \(8\), co w tym przypadku daje odpowiedź \(3\).
W jaki sposób logarytmy ułatwiają obliczenia w codziennym życiu?
Logarytmy przydają się w codziennym życiu w różnych dziedzinach, takich jak finanse i nauka. Umożliwiają one szybsze zrozumienie zmian w bilansie finansowym czy analizy wzrostu, co oszczędza czas podczas obliczeń.
Jakie techniki można zastosować przy obliczaniu trudniejszych logarytmów?
Przy obliczaniu trudniejszych logarytmów warto używać wzorów logarytmicznych oraz przekształcać liczby do postaci potęg. Przykładowo, dla logarytmu \( \log_{4} \frac{1}{2} \), można zamienić ułamek na formę potęgi, co znacznie ułatwi dalsze obliczenia.
W jakich dziedzinach nauki logarytmy mają istotne zastosowanie?
Logarytmy mają szerokie zastosowanie w takich dziedzinach jak fizyka, biologia i technologia. Na przykład w fizyce są używane do obliczania natężenia dźwięku, a w biologii do modelowania wzrostu populacji.
Jakie narzędzia mogą pomóc w obliczaniu logarytmów?
W obliczeniach logarytmicznych pomocne mogą być kalkulatory logarytmiczne oraz dostępne w Internecie narzędzia online. Te programy umożliwiają szybkie i łatwe wykonywanie obliczeń, często z dodatkowymi wyjaśnieniami i przykładami.