Witaj w fascynującym świecie równań sprzecznych! Zanim jednak zaczniemy odkrywać ich intrygujące tajemnice, zatrzymajmy się na chwilę, aby zdefiniować ten pojęcie. Równanie sprzeczne działa jak „matematyczny wariat”, ponieważ po odpowiednich przekształceniach prowadzi nas do oczywistej fałszywej równości. Wyobraź sobie, że natrafiłeś na równanie 0=1 lub 3=5 – w takim przypadku musisz przyznać, że coś tu zdecydowanie nie gra. Takie równania nie mają żadnych rozwiązań w zbiorze liczb rzeczywistych, co sprawia, że sprzeczności te krążą w kręgach algebry jak niezaproszeni goście na weselu.
- Równania sprzeczne prowadzą do fałszywych równości, co oznacza brak jakiegokolwiek rozwiązania.
- W przeciwieństwie do równań oznaczonych (jedno rozwiązanie) i tożsamościowych (zawsze prawdziwe), równania sprzeczne nie mają szansy na współpracę w matematycznej rzeczywistości.
- Unikanie równań sprzecznych wymaga weryfikacji danych, analizy relacji między zmiennymi oraz regularnych przekształceń równań.
- Graficzne przedstawienie równań, takie jak równoległe linie, może pomóc w dostrzeganiu sprzeczności.
- Równania sprzeczne uczą krytycznego myślenia oraz uwrażliwiają na błędne założenia w matematyce i naukach ścisłych.
- Przykłady sprzecznych równań ilustrują, jak błędne założenia mogą prowadzić do frustrujących wyników, np. 2x + 3 = 2x + 5 prowadzi do 3 = 5.
- Równania sprzeczne mają zastosowanie nie tylko w matematyce, ale także w inżynierii, ekonomii i fizyce, gdzie mogą prowadzić do niebezpiecznych sytuacji.
Równania sprzeczne stanowią nie tylko czyste abstrakcje; ich zrozumienie w istotny sposób przyczynia się do efektywnego rozwiązywania problemów matematycznych. Uczymy się z nich nie tylko o samej matematyce, lecz również o krytycznym myśleniu i dokładności. Mówiąc prościej, napotkanie takiego równania często sygnalizuje, że gdzieś po drodze pomieszały nam się założenia, dane lub inne kluczowe elementy. Z pewnością nie chcesz, aby Twoje równania kończyły się na fałszywej równości – to oznacza, że Twoje dane były albo pełne sprzeczności, albo po prostu wymyśliłeś coś zupełnie absurdalnego!
Kluczowe Cechy Równań Sprzecznych
Teraz spróbujmy odróżnić równania sprzeczne od ich „kolegów”: równań oznaczonych oraz tożsamościowych. Równania oznaczone mają dokładnie jedno rozwiązanie, co jest dość tradycyjne. Z kolei równania tożsamościowe zachowują się jak prawdziwe kokietki – są zawsze prawdziwe dla każdego możliwego „x”. W przeciwieństwie do tych równaniom, równania sprzeczne całkowicie odrzucają możliwość istnienia jakiegokolwiek rozwiązania. Generalnie rzecz biorąc, gdy nasze działania prowadzą do wyniku w stylu 0=1, możemy być pewni, że do matematyki zaprosiliśmy sprzeczność!
Ostatnia rzecz, którą musisz mieć na uwadze, to że równania sprzeczne różnią się diametralnie od równań tożsamościowych. To jak różnica między prawdziwym prosciutto a przypominającą je szynką ze sklepu spożywczego – jedna to prawdziwy rarytas, a druga niekoniecznie! W praktyce każda sprzeczność może przekładać się na różne aspekty życia codziennego, takie jak zarządzanie budżetem domowym, kiedy to wydatki przewyższają wpływy. Ucz się na błędach równań sprzecznych, a może uda Ci się uniknąć podobnych pułapek w realnym świecie! Pozwól, aby matematyka stała się Twoim sprzymierzeńcem, a sprzeczność – alarmującym sygnałem do przemyśleń!
| Pojęcie | Definicja |
|---|---|
| Równanie sprzeczne | Równanie, które po przekształceniu prowadzi do fałszywej równości, np. 0=1 lub 3=5. |
| Równania oznaczone | Równania posiadające dokładnie jedno rozwiązanie. |
| Równania tożsamościowe | Równania, które są zawsze prawdziwe dla każdego możliwego „x”. |
Najczęstsze błędy w rozwiązywaniu równań sprzecznych: Jak ich unikać?
Równania sprzeczne, o których mowa, przypominają matematyczne potwory, które po licznych przekształceniach prowadzą nas na manowce. Mówiąc krótko, uczciwe kalkulacje mogą kończyć się absurdalnymi wynikami, takimi jak 0=1. Tego rodzaju problemy spotykasz wszędzie, gdzie tylko się obrócisz! Jednak jak ich unikać? Wygląda to jak gra w chowanego z matematycznymi pułapkami – trzeba być czujnym i uważać, by nie wpaść w sprzeczne sidła. Na szczęście mam dla Ciebie kilka wskazówek, które pozwolą Ci nie wchodzić w interakcje ze sprzecznymi równościami.
Jak nie dać się wpisać na listę sprzeczności
Na początku zweryfikuj dokładnie wszystkie dane, z których korzystasz w swoim równaniu. Wiesz, jak to bywa – przyswajasz wiedzę na pamięć, a w gorączce poszukiwania wymarzonego rozwiązania zapominasz sprawdzić, czy nie mieszasz jabłek z gruszkami. Po drugie, zwróć uwagę na relacje między zmiennymi. Tworzenie równości powinno przypominać taniec, a nie chaotyczny balet; każda zmienna musi harmonijnie współgrać z pozostałymi, jak w idealnym duecie tanecznym. Co więcej, regularne przekształcenia są istotne – czasem wystarczy proste dodawanie lub odejmowanie, aby rozwiązać problem, a Ty możesz nie zdawać sobie sprawy, że zmierzasz ku ukrytej sprzeczności.
- Zweryfikuj wszystkie dane i ich źródła.
- Sprawdź relacje między zmiennymi, aby uniknąć chaotycznych wyników.
- Regularnie przekształcaj równania, by zauważyć ewentualne sprzeczności.
Graficzne obliczenia
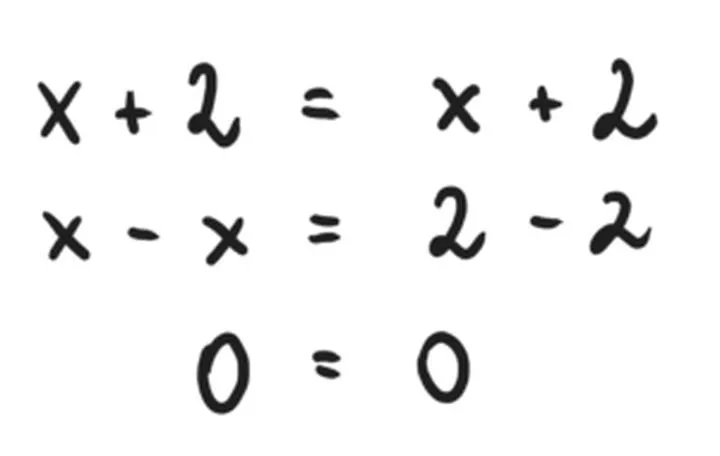
Nie lekceważ także graficznych interpretacji równań! Czasami jedno spojrzenie na wykres oszczędza mnóstwo czasu oraz nerwów. Jeśli dostrzegasz równoległe linie w swoim układzie równań, warto natychmiast podjąć działania, ponieważ to oznacza, że brak punktu wspólnego! Pamiętaj również o dziedzinie równań, szczególnie w przypadku równań wymiernych. Niezbyt mądrze będzie szukać rozwiązania dla x, które równa się zerosumie – nikt nie pragnie trzymać się pustki!
Pamiętając o tych kilku zasadach, zyskujesz szansę na unikanie sprzecznych równań niczym diabeł święconej wody. Nie daj się złapać w pułapkę matematycznych sprzeczności, bo ostatecznie, czymże jest życie bez przygód do rozwiązania? Równania sprzeczne to nie tylko pułapki, ale także lekcje pokory oraz nauka dostrzegania błędów. A w matematyce, podobnie jak w życiu, błędy stanowią niegrzeszne fakty – wszyscy je popełniamy!
Przykłady równań sprzecznych: Analiza i interpretacja wyników
Równania sprzeczne stanowią ciekawe matematyczne zjawisko, które odzwierciedla naszą zdolność do tworzenia nieosiągalnych oczekiwań. Wyobraźcie sobie, że chcemy udowodnić, iż 0 równa się 1. Takie próby nie przynoszą mądrości życiowej; zamiast tego zwykle doprowadzają do siedzenia z kubkiem herbaty nad absurdalnymi stwierdzeniami. Równanie sprzeczne powstaje z błędnych założeń, które po przeprowadzeniu wszystkich magicznych operacji algebraicznych prowadzą do fałszywych równości, jak 0=1. Co z tego wynika? Nic, ponieważ nie istnieje liczba, która mogłaby podjąć się takiego wyzwania!
Przykładem takiego równania sprzecznego może być chociażby 2x + 3 = 2x + 5. Kiedy odejmiemy 2x od obu stron, uzyskujemy absurdalne stwierdzenie 3 = 5. Z pewnością każdy przyzna, że te liczby nie mają szans na współpracę w matematycznej rzeczywistości! Równania sprzeczne nie tylko oferują brak rozwiązań, ale przypominają także, że są jak nieosiągalny cel, wywołujący jedynie frustrację. Niemniej jednak, warto dostrzegać w tym doskonałą okazję do rozwijania krytycznego myślenia oraz unikania błędów w bardziej skomplikowanych obliczeniach.
Kluczowe cechy równań sprzecznych
Równania sprzeczne charakteryzują się kilkoma istotnymi cechami, które mogą okazać się przydatne w matematycznych rozważaniach. Po pierwsze, prowadzą do fałszywych stwierdzeń oraz oznaczają brak jakiegokolwiek rozwiązania. W graficznym świecie reprezentują je dwie równoległe linie, które nigdy się nie spotkają – to idealne wyobrażenie dla tych, którzy pragną być w dwóch miejscach jednocześnie, ale niestety jest to niemożliwe! W praktyce spotkanie sprzecznych założeń przypomina próbę skoszenia trawnika w deszczu: choć wiemy, że to nie ma sensu, ostrza wciąż obracają się z beznadziejną nadzieją.
Wyjątkowość równań sprzecznych ujawnia się również w ich praktycznych konsekwencjach. W życiu codziennym wielokrotnie napotykamy sprzeczności; na przykład, gdy suma wydatków na budżet przekracza nasze możliwości finansowe. Takie sytuacje przypominają nam, że niektóre modele są tak nierealistyczne, że jedyne, co pozostaje, to śmiech z frustracji. Uczy nas to, że warto dokładnie przemyśleć swoje założenia i pozostać czujnym, ponieważ matematyka to nie tylko suche liczby, ale także sztuka logicznego myślenia, która czasami zaskakuje nas nieprzyjemnymi niespodziankami! Niech to będzie lekcja pokory w obliczu równań sprzecznych!
Zastosowania równań sprzecznych w matematyce i naukach ścisłych
Równania sprzeczne stanowią prawdziwie enigmatyczne zjawiska w matematyce. Można je porównać do czarnej dziury równań, w którą wpadają wszystkie nasze nadzieje na znalezienie rozwiązania. Czym tak właściwie są te niezwykłe zjawiska? Wyobraź sobie, że pełnisz rolę detektywa matematycznego, a twoim zadaniem staje się analiza opóźnionej kolizji między dwiema liniami prostymi. Mimo wnikliwej analizy logiki, dojdziesz do absurdalnej konkluzji, według której \(0\) rzekomo może być równe \(1\). Jeśli cię to zdumiało i przekroczyło jakiekolwiek granice zdrowego rozsądku, to właśnie natrafiłeś na równanie sprzeczne, które nie ma żadnych rozwiązań!
Równania sprzeczne pełnią nie tylko rolę matematycznego wyzwania, ale także stają się doskonałym nauczycielem. Uczą nas krytycznego myślenia o założeniach problemów oraz sygnalizują błędy w modelowaniu. Wyobraź sobie, że planujesz swoją przyszłość finansową, ale twoje wydatki na ukończenie studiów znacznie przewyższają twój aktualny budżet. W tym momencie matematyka, z równaniami sprzecznymi, pokazuje, że twoje dane stanowią wielki mit; realizacja niespełnionych marzeń w obecnych warunkach staje się niemożliwa. Każdy detektyw wie, że najlepiej zwalczać sprzeczności, zanim wyruszymy na nielegalne poszukiwania rozwiązania!
Równania sprzeczne w naukach ścisłych
Matematyka nie jest jedyną dziedziną, w której równania sprzeczne mają znaczenie. Inżynieria, ekonomia a nawet fizyka wciąż obfitują w sprzeczne wyrażenia. Na przykład, podczas budowy mostu, modelując jego nośność, każda fałszywa przesłanka prowadzi do pojawienia się sprzeczności matematycznych. Nie można traktować tego osobiste, lecz opuszczony most to nie jest miejsce, w jakim chcesz mieć do czynienia z równaniami sprzecznymi. Wystarczy spróbować podnieść na sobie bezsensowne obciążenie – wtedy z przekonaniem odkryjesz, że twoje równania krzyczą „nie da się!”.
Reasumując, odkrywanie równań sprzecznych przynosi wiele korzyści. Działają one jak alarm przeciwpożarowy, ucząc nasze dzieci unikać pułapek logicznych oraz wzmacniając w nich wyczulenie na potencjalne błędy w obliczeniach. Warto zatem poznać ich naturę – sprzeczność nie staje się wrogiem, lecz przyjacielem, który otwiera drzwi do nowych wniosków i prawidłowych modeli. Zatem następnym razem, gdy napotkasz równanie sprzeczne, nie zniechęcaj się – przytul je i wyciągnij cenną naukę na przyszłość! Matematyka w końcu stanowi sztukę logicznego myślenia, a równania sprzeczne to tylko „gdybanie” w niezwykłym, matematycznym wszechświecie.
- Równania sprzeczne w inżynierii mogą prowadzić do niebezpiecznych konstrukcji.
- W ekonomii, błędne założenia mogą narażać projekty na straty finansowe.
- Fizyka z równaniami sprzecznymi może zniekształcać opis rzeczywistości.

Lista powyżej przedstawia przykłady dziedzin, gdzie równania sprzeczne mogą prowadzić do poważnych problemów.
Źródła:
- https://kalkulator.org.pl/blog/co-to-jest-rownanie-sprzeczne-kompleksowy-przewodnik-po-matematycznych-paradoksach
- https://www.matemaks.pl/rownanie-oznaczone-tozsamosciowe-i-sprzeczne.html
- https://szaloneliczby.pl/rownanie-oznaczone-tozsamosciowe-i-sprzeczne/
Pytania i odpowiedzi
Co to jest równanie sprzeczne?
Równanie sprzeczne to takie, które po przekształceniach prowadzi do fałszywej równości, np. 0=1 lub 3=5. Oznacza to, że nie ma żadnych rozwiązań w zbiorze liczb rzeczywistych.
Jakie są kluczowe cechy równań sprzecznych?
Równania sprzeczne charakteryzują się brakiem jakiegokolwiek rozwiązania i prowadzą do oczywistych fałszywych stwierdzeń, jak 3=5. W graficznym przedstawieniu reprezentują je równoległe linie, które nigdy się nie spotkają.
Jakie błędy najczęściej prowadzą do równań sprzecznych?
Do równań sprzecznych często prowadzi niewłaściwe zweryfikowanie danych lub pomieszanie relacji między zmiennymi. Kluczowe jest również wykonywanie regularnych przekształceń, aby zauważyć ewentualne sprzeczności na wczesnym etapie.
W jaki sposób równania sprzeczne mogą pomóc w nauce matematyki?
Równania sprzeczne pomagają rozwijać krytyczne myślenie oraz uczą analizy założeń problemu. Używanie ich jako narzędzia do identyfikacji błędów pozwala lepiej zrozumieć zasady matematyczne i unikać podobnych pułapek w przyszłości.
Jakie są praktyczne konsekwencje równań sprzecznych w życiu codziennym?
Równania sprzeczne mogą odzwierciedlać nieosiągalne oczekiwania w różnych sytuacjach życiowych, np. w zarządzaniu budżetem. Wskazują na nierealistyczne założenia, które mogą prowadzić do frustracji i niepowodzeń w planowaniu.