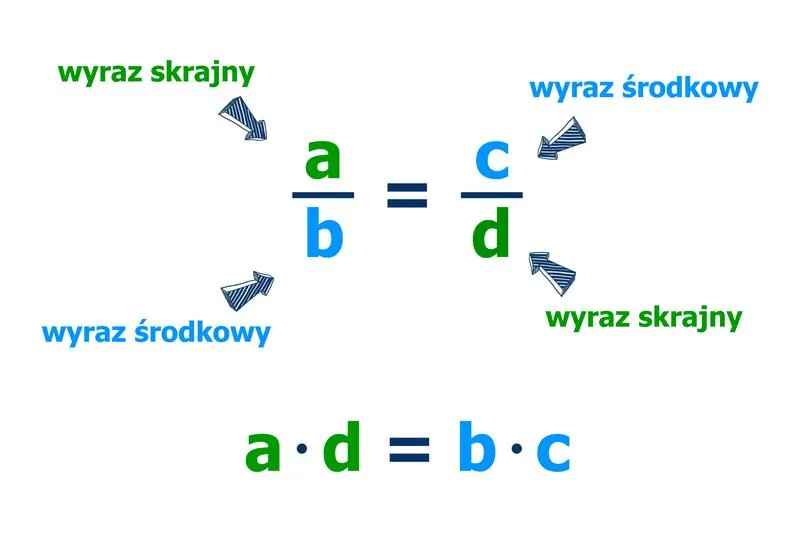
Równości algebraiczne przypominają spotkania w piaskownicy, gdzie liczby i zmienne bawią się razem. Wyobraź sobie, że dysponujesz magicznym zaklęciem, które brzmi: „Witaj, dziś jesteśmy równo 3x!” W tym przypadku „3x” stanowi naszą tajną recepturę, a inne wyrażenia muszą podjąć wyzwanie i dorównać temu standardowi. Ale co właściwie to oznacza? Równanie „a = 3x” wskazuje, że cokolwiek kryje się za „a”, ma mieć tę samą wartość co „3x”, czyli liczbę, która powstaje w momencie, gdy pomnożymy naszą niewiadomą x przez 3.
Jak rozgryźć algebraiczne zagadki?
W świecie matematyki zmienne pełnią rolę podobną do aktorów w teatralnej sztuce. Nasza postać „x” musi zagrać świetnie, aby zadowolić wrażliwego reżysera, którym jest liczba 3. Z pewnością zauważasz, że „3x” to wyrażenie, które oferuje więcej niż tylko prostą prostą — otwiera przed nami całe spektrum możliwości. Weźmy na przykład sytuację, w której „x” przyjmuje wartość 2; wtedy „3x” staje się… 6! W rezultacie, aby uzyskać „akceptację” równości, wyrażenie musiałoby błyszczeć na poziomie 6, zamiast nudnych 4.
Przypadkowe sąsiadki – algebraiczne wyrażenia
Równości można postrzegać jak przyjaźń — są trwałe, ale w każdej chwili mogą stanąć w obliczu próby. Wyrażenia algebraiczne zaskakują nas jak niespodziewani goście i mogą przyjmować różnorodne formy. Nasze „3x” może być poprzedzone mnóstwem dodatków, takich jak „2x + 4” czy „8x - 5”. Wiesz, jak to bywa — czasem jeden z gości musi ustąpić miejsca, aby inni mogli wejść. W takim razie powinniśmy wytrwale manipulować naszymi wyrażeniami, by każda strona mogła zawołać: „Jestem równo 3x!”
Na zakończenie dnia, zrozumienie równości przypomina ciekawe przygody, w których każda zmienna ma swoją opowieść do przekazania. Pamiętaj, że równości nie są straszne! Stanowią one grę w karty, gdzie każda karta ma określoną rolę do odegrania. Im więcej praktyki, tym lepiej zrozumiemy, że każdy zestaw wyrażeń skrywa potencjał zaskoczenia nas swoją wartością. A może pewnego dnia odkryjesz, że pozwalają one spojrzeć na świat w zupełnie nowym świetle! Czas na algebraiczne zabawy!
Przykłady wyrażeń algebraicznych i ich możliwe równości - analiza krok po kroku
Wyrażenia algebraiczne przypominają tajemnicze przepisy kulinarne — pełne symboli i nieco enigmatyczne. Jednak po dodaniu odpowiednich składników otrzymujemy smaczną potrawę matematyczną. Na przykład weźmy wyrażenie \(3x + 5\). Czymże może być to wyrażenie, jeśli nie sumą trzech razy nieznanej zmiennej x oraz pięciu? Porównajmy to do dodawania trzech jabłek do pięciu gruszek. Jeśli tylko uda nam się znaleźć wartość \(x\), bez trudu określimy liczbę owoców w naszej tajemniczej torbie! To wyrażenie stanowi doskonały przykład na początek naszej algebraicznej podróży.
W momencie, gdy przyjrzeliśmy się już prostemu wyrażeniu, czas na nieco bardziej skomplikowaną sprawę. Powiedzmy, że stykamy się z równaniem \(2x^2 - 4x + 2 = 0\). To przypomina przepis na ciasto, gdzie w składnikach znajdziemy nie tylko x, lecz także jego kwadrat! Rozwiązując takie równanie, przenosimy się do magicznego świata wyznaczania miejsc zerowych. Możemy podjąć wyzwanie i zastosować wzory kwadratowe lub faktoryzację, aby odsłonić naszą cukierkową zagadkę.
Jak radzić sobie z równaniami?

Gdy już wyczołgaliśmy się przez kręte ścieżki algebraicznych wyrażeń, warto zgłębić temat równości algebraicznych. Na przykład równanie \(x + 7 = 10\) to coś, co można rozwiązać niemal w mgnieniu oka. Wystarczy odjąć 7 od obu stron równania i voila! Otrzymujemy, że \(x = 3\). To jak przeprowadzka w małym mieszkaniu — czasami wystarczy tylko najprostsza zmiana, aby wszystko zaczęło działać. Równości stanowią kluczowe narzędzie w naszym algebraicznym arsenale, pozwalając sprawnie współpracować z zmiennymi oraz odkrywać niezbędne wartości. Równania to nie tylko zimne liczby, lecz raczej małe dramy i rozczarowania, które mogą prowadzić do wielkich odkryć!
- Równania liniowe – podstawowy typ równań, który można łatwo rozwiązać.
- Równania kwadratowe – wymagają zastosowania wzorów kwadratowych lub faktoryzacji.
- Równania wielomianowe – bardziej złożone formy wymagające różnorodnych metod rozwiązywania.
Wszystkie te rodzaje równań mają swoje unikalne cechy i metody rozwiązania, które warto poznać.
Na koniec warto przypomnieć sobie, że wyrażenia algebraiczne i równania są ze sobą ściśle związane. Każda zmiana w wyrażeniu wywiera wpływ na równanie, a każde rozwiązanie równania dodaje nowy wymiar do naszego algebraicznego świata. Dlatego, gdy następnym razem zanurzysz się w sięgające nieba 'x' i 'y', pamiętaj — to nie tylko abstrakcyjne znaki, ale klucz do niekończącej się zabawy w rozwiązywaniu zagadek! Trzymaj się mocno swojego kalkulatora, bo algebra to naprawdę niezwykła wyprawa!
Dlaczego ważne jest rozpoznawanie równości w matematyce: Praktyczne zastosowania

Równości w matematyce przypominają tajemnice, które czekają na odkrycie. Gdy wchodzimy w świat liczb oraz ich relacji, dostrzegamy, że równości nie są jedynie nudnymi symbolami, lecz także potężnymi narzędziami, mogącymi znacząco ułatwić nam życie. Ich wyjątkowa moc pomaga nam nie tylko zrozumieć algorytmy, ale również skutecznie radzić sobie z codziennymi zadaniami, takimi jak obliczanie budżetu domowego czy ustalanie harmonogramu dnia. Czyż to nie brzmi jak magia? Takie umiejętności przypominają supermoce, o ile potrafimy zrozumieć znaczenie tych wszystkich znaków!
Niemniej jednak, to jeszcze nie koniec! Rozpoznawanie równości w matematyce rozwija nasze umiejętności logicznego myślenia. Każda równość staje się dla nas małą łamigłówką do rozwiązania. Wyobraź sobie, że siedzisz w kawiarni, starając się obliczyć, ile kawy możesz wypić, nie narażając się na bankructwo. Dzięki zrozumieniu, w jaki sposób różne zjawiska są ze sobą powiązane, przekształcamy złożone problemy w proste, zrozumiałe zadania. Kto by pomyślał, że matematyka może mieć tak praktyczne zastosowanie i jednocześnie okazać się przydatna w życiu codziennym!
Równości i ich wpływ na podejmowanie decyzji
Kiedy zaczynamy zyskiwać wiedzę na temat równości, zaczynamy myśleć w sposób bardziej analityczny. Na przykład, podejmując decyzje inwestycyjne, zrozumienie równości pomaga nam w szacowaniu potencjalnych zysków oraz strat. Mówiąc wprost, jesteśmy w stanie ocenić, czy nasze pieniądze pracują wydajnie, czy może lepiej je odłożyć na później. Klucz do podejmowania lepszych decyzji finansowych tkwi w zrozumieniu równości, co z pewnością uratuje nas przed wieloma kłopotami! Nikt z nas nie chciałby, aby jego oszczędności zniknęły jak pieniądze czarodzieja wciągane w głąb ziemi.
Co więcej, równości mają zastosowanie nie tylko w matematyce, ale właściwie w każdej dziedzinie życia! Spotykamy je w grafice komputerowej, gdy przeliczamy piksele, czy też w naukach przyrodniczych, kiedy staramy się zrozumieć zjawiska zachodzące wokół nas. Dlatego rozpoznawanie równości w matematyce nie stanowi jedynie modnego trendu dla pasjonatów „cyferkowania”, lecz jest absolutną koniecznością dla wszystkich, którzy chcą sprostać wyzwaniom współczesnego świata. Pamiętaj, im lepiej opanujesz równości, tym mniejsza szansa, że będziesz o nich myślał z przerażeniem, jak o egzaminie z matematyki w szkole podstawowej!
Błędy w obliczeniach: Jak nie dać się zwieść fałszywym równościom algebraicznym
W świecie matematyki, zwłaszcza w algebrze, równości stanowią temat o ogromnej wartości. Jednak nie dajcie się zwieść! Od czasu do czasu, zamiast natrafić na złoty skarb, spotykamy pułapki fałszywych równości, które mogą nas wyprowadzić w maliny. Warto pamiętać, że nie każda równość jest tak oczywista, jak się na pierwszy rząd wydaje. Zgubienie się w zawiłościach algebraicznych przypomina błądzenie w lesie bez mapy – z tą różnicą, że w lesie przynajmniej nietoperze nie próbują nas wprowadzić w błąd.
Jednym z najczęściej popełnianych błędów przez uczniów, a także osoby nieco bardziej doświadczone, jest niewłaściwe manipulowanie równościami. Czasami można odnieść wrażenie, że wystarczy jedynie przesunąć kilka liczb, dodać coś od siebie, a gotowa odpowiedź zaraz się pojawi! Niestety rzeczywistość bywa inna, bo każda operacja wymaga staranności. W przeciwnym razie możemy skończyć próbując rozwiązać równanie, które ledwo ma cokolwiek wspólnego z naszymi pierwotnymi danymi – a to naprawdę może być frustrujące i zniechęcające.
Uważaj na pułapki!
Innym klasykiem w błędach matematycznych staje się ryzyko nieprecyzyjnego przycinania równań. Wygląda na to, że porównanie składników z lewej i prawej strony to zadanie łatwe, ale nie każdy zdaje sobie sprawę, że czasami usunięcie składnika potrafi całkowicie zmienić charakter równania. Można powiedzieć, że algebra przypomina grę w Tetris – musisz zachować czujność, aby niczego nie zablokować, bo w przeciwnym razie nie będziesz miał już gdzie grać. Dlatego pamiętajcie o konsekwencjach, jakie niosą wasze decyzje matematyczne!
Na końcu, warto zwrócić uwagę na kilka kluczowych zagadnień dotyczących manipulacji równościami:
- Dokładność w przekształceniach – każda operacja musi być przemyślana.
- Ścisłe porównanie składników – upewnij się, że porównujesz odpowiednie elementy.
- Analiza konsekwencji – przemyśl, jakie będą skutki twoich działań w równaniu.
Na koniec, nie zapominajcie, że praktyka czyni mistrza. Równania wydające się proste mogą nas zaskoczyć, dlatego warto analizować je z różnych perspektyw. Każde zadanie przypomina zagadkę – złe posunięcie często prowadzi do fałszywego tropu w kryminale. Zamiast opierać się na fałszywych równości, lepiej zainwestować czas w zrozumienie, dlaczego coś działa, a coś innego nie. Dzięki temu nie tylko rozwiążecie zadania, ale także zadbacie o swoje matematyczne bezpieczeństwo!
Błąd |
Opis |
|---|---|
Niewłaściwe manipulowanie równościami |
Przesuwanie liczb i dodawanie elementów bez staranności, co prowadzi do błędnych wyników. |
Nieprecyzyjne przycinanie równań |
Usunięcie składnika może zmienić charakter równania, co wymaga ścisłej uwagi podczas porównywania stron. |
Pytania i odpowiedzi
Jakie znaczenie ma wyrażenie "3x" w kontekście równości algebraicznych?
Wyrażenie "3x" symbolizuje wartość, która powstaje w momencie, gdy zmienna x jest pomnożona przez 3. Równanie "a = 3x" oznacza, że wartość zmiennej a jest równa trzykrotności zmiennej x, co jest kluczowe w przekształceniach algebraicznych.
W jaki sposób zmienna x wpływa na wartość wyrażenia "3x"?
Wartość "3x" zmienia się w zależności od wybranej wartości zmiennej x. Na przykład, jeśli x wynosi 2, "3x" daje wynik 6, co ilustruje, jak różne wartości x wpływają na ostateczny rezultat wyrażenia.
Jakie inne wyrażenia algebraiczne mogą być równe "3x"?
Inne wyrażenia, takie jak "6x - 3x" lub "2x + 4", mogą również być równe "3x", jednak muszą być prawidłowo uproszczone lub przekształcone. Proces ten przypomina dążenie do uzyskania równowagi w algebraicznych grach z równaniami.
Dlaczego ważne jest zrozumienie równości w codziennym życiu?
Zrozumienie równości algebraicznych pozwala nam korzystać z matematyki w praktycznych sytuacjach, takich jak zarządzanie budżetem czy podejmowanie decyzji inwestycyjnych. Dzięki tej wiedzy możemy efektywnie rozwiązywać problemy i analizować różne zjawiska.
Jakie są najczęstsze błędy popełniane w manipulacjach algebraicznych?
Najczęstsze błędy obejmują niewłaściwe manipulowanie równościami oraz nieprecyzyjne przycinanie równań. Takie pomyłki mogą prowadzić do całkowicie błędnych wyników, dlatego ważna jest staranność i dokładność w każdej operacji matematycznej.