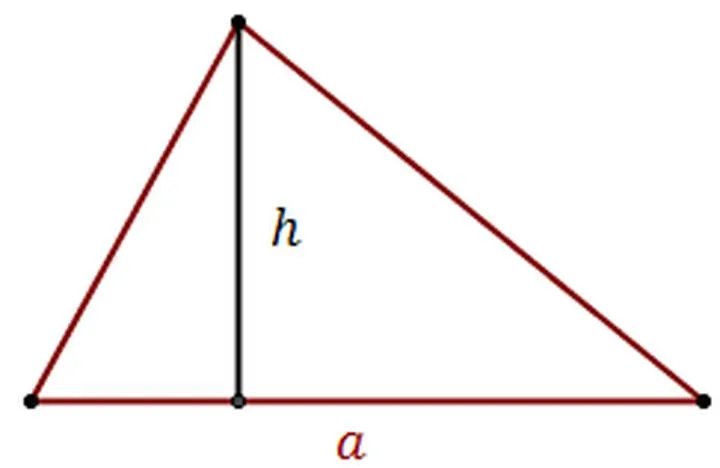
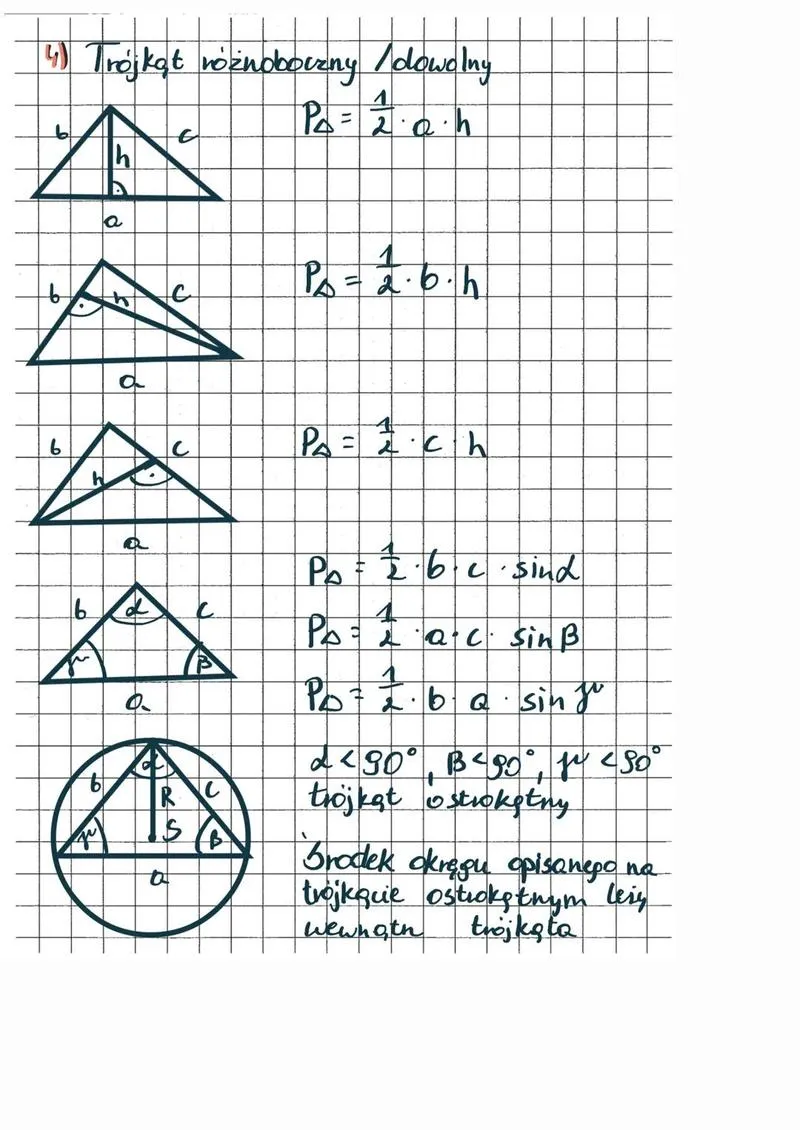
Trójkąty stanowią jedne z najfajniejszych figur geometrycznych, jakie możemy spotkać w naszym otoczeniu. Te figury mają swój niepowtarzalny urok, mimo że, jak to zwykle w życiu bywa, wymagają od nas nieco matematycznej pikanterii. Wśród najważniejszych zadań, jakie stawiają przed nami trójkąty, znajduje się obliczenie pola. Na szczęście mamy do dyspozycji kilka sposobów, które pozwolą nam z łatwością się z tym uporać. Tradycyjny, a jednocześnie niezawodny wzór to \( P = \frac{1}{2}ah \), gdzie \(a\) oznacza długość boku, a \(h\) to wysokość. Porównując to do przepisu na ulubione ciasto, można powiedzieć, że jest prosty, a jednocześnie skuteczny!
- Trójkąty są fascynującymi figurami geometrycznymi wymagającymi obliczeń pola.
- Klasyczny wzór na pole trójkąta to \( P = \frac{1}{2}ah \), gdzie \(a\) to bok, a \(h\) to wysokość.
- Alternatywny wzór to \( P = \frac{1}{2}ab\sin \gamma \), kiedy znamy długości dwóch boków i kąt między nimi.
- Wzór Herona \( P = \sqrt{p(p-a)(p-b)(p-c)} \) pozwala obliczyć pole znając tylko długości boków.
- Obliczenia można również wykonać za pomocą wzoru \( P = \frac{abc}{4R} \), uwzględniając promień okręgu opisanego.
- Wzór na pole trójkąta równobocznego to \( P = \frac{\sqrt{3}}{4}a^2 \), co pozwala na łatwe obliczenia znając tylko jeden bok.
- Nowoczesne metody obliczania to m.in. metoda Sarusa oraz obliczenia wykorzystujące współrzędne w przestrzeni R3.
- Najczęstsze błędy przy obliczaniu pola to zapominanie o wysokości, wybór niewłaściwego wzoru i mieszanie narzędzi matematycznych.
- Obliczanie pola trójkąta ma praktyczne zastosowanie w życiu codziennym, w architekturze i przy organizacji przestrzeni.
Co jednak zrobić, gdy nie mamy pod ręką wysokości? Nie martwcie się, ponieważ istnieje możliwość skorzystania ze wzoru, który wymaga nieco więcej informacji, ale ma w sobie magnię kątów. Ten wzór, znany wszystkim miłośnikom geografii, to \( P = \frac{1}{2}ab\sin \gamma \). W tym przypadku, zamiast wysokości, wykorzystujemy długości dwóch boków \(a\) i \(b\) oraz kąt \( \gamma \) znajdujący się między nimi. Prawda, że brzmi jak zaklęcie? Rzucamy więc czarującą formułę! :)
Co zrobić, gdy mamy tylko boki trójkąta?
Nie ma wątpliwości, że możemy znaleźć się w sytuacji, w której dostępne będą jedynie długości boków trójkąta. W takim przypadku z pomocą przychodzi wzór Herona, czyli \( P = \sqrt{p(p-a)(p-b)(p-c)} \), gdzie \(p\) to połowa obwodu trójkąta. To przypomina grę w zgadywanie, w której czujemy się jak detektywi odkrywający tajemnice ukryte w bokach. Wystarczy znać długości, a potem policzyć \(p\) i voilà! Otrzymujemy pole trójkąta niczym na talerzu!
Dodatkowo, wielcy matematyczni czarodzieje pomyśleli również o okręgach! Wzór \( P = \frac{abc}{4R} \) przyciąga uwagę tych, którzy pragną podążać za krzywymi. W tym przypadku bierzemy pod uwagę długości boków oraz promień okręgu opisanego, który wygląda jak gwiazda na nocnym niebie! Jak więc można łatwo zauważyć, pole trójkąta oferuje niezliczone możliwości, a korzystając z jednego z tych wzorów, możemy z dumą, niczym matematyczny Gandalf, ogłosić: „Znam pole trójkąta!”
Innowacyjne metody obliczania pola trójkąta: Od klasycznych technik po nowoczesne podejścia
Odkrywanie różnorodnych metod obliczania pola trójkąta zdecydowanie przynosi niesamowite emocje! Na przestrzeni wieków matematycy nieustannie modyfikowali swoje podejście do tej z pozoru prostej figury, która, jak się okazuje, skrywa wiele tajemnic. Rozpoczynając od klasycznego wzoru, który polega na obliczeniu połowy iloczynu długości boku oraz wysokości, matematycy szybko zrozumieli, że to jedynie początek fascynującej podróży. Definitywnie możliwość obliczeń w tej dziedzinie ma tyle odmian, ile różnorodnych sukienek znajduje się w szafie każdej miłośniczki mody. Tak więc, czy jesteście gotowi na matematyczną przygodę?
Pamiętajcie, że wzór na pole trójkąta to dopiero wstęp – istnieje również wzór Herona, który przypomina magiczną recepturę na ciasto. Najpierw zbieramy wszystkie składniki, czyli długości boków, następnie łączymy je z połową obwodu (p), a na koniec wyciągamy aromatyczną powierzchnię trójkąta z piekarnika równości matematycznych! Jednakże, warto wspomnieć, że wśród naszych matematycznych trików znajduje się wiele nowoczesnych technik, które przyciągają coraz większą rzeszę pasjonatów matematyki. Razem z entuzjazmem odkrywcy możemy rzucić się w wir bardziej nowatorskich podejść do tych obliczeń!
Nowoczesne podejścia do obliczenia pola trójkąta
Nie daj się zwieść myśli, że wzory zarezerwowane są jedynie dla nudnych przykładów w podręcznikach! Dzięki nowoczesnej technologii obliczanie pola trójkąta zyskuje nowy wymiar ekscytacji. Wyobraź sobie, jak wykorzystujesz współrzędne w przestrzeni R3 do obliczenia pola trójkąta, niczym matematyczny czarodziej w własnym labiryncie. Co więcej, metody takie jak metoda Sarusa wyłaniają się z magicznego kapelusza matematyki, oferując świeże możliwości na osiągnięcie pożądanej powierzchni w niezwykle stylowy sposób!
Poniżej przedstawiam kilka nowoczesnych metod obliczania pola trójkąta:
- Metoda współrzędnych w R3
- Wzór Herona
- Metoda Sarusa
- Obliczenia z wykorzystaniem macierzy
Na zakończenie, nie możemy zapomnieć o dumie, którą odczuwamy, gdy z łatwością wykonujemy te obliczenia. Połowa obwodu przypomina serdeczne przytulenie przyjaciela, wzór na sinus stanowi klucz do zrozumienia duszy kąta, a nasze kalkulatory są jak niezawodne przyjaciółki, zawsze gotowe wspierać nas w trudnych chwilach. W matematyce nie istnieją rzeczy niemożliwe, a każda łamigłówka staje się okazją do zaprezentowania swojego matematycznego geniuszu. Dlatego, drodzy przyjaciele, obliczanie pola trójkąta nie tylko nabiera cech nauki, ale wręcz staje się prawdziwą sztuką, a my jesteśmy artystami, którzy z pasją posługują się matematycznymi pędzlami!
Przykłady praktycznego zastosowania obliczeń pola trójkąta w codziennym życiu
Obliczenia pola trójkąta to temat, który napotykasz niemal wszędzie! Może nie zdajesz sobie z tego sprawy, ale za każdym razem, gdy rysujesz na kartce schemat z trójkątami (a kto z nas tego nie robi?), wkraczasz w fascynujący świat matematycznych obliczeń. Możliwe, że nie każdy dostrzega w tym sens, ale wyobraź sobie, że pełnisz rolę projektanta swojego ogródka. Przed posadzeniem ulubionych kwiatków musisz najpierw ustalić, ile miejsca zajmie rabatka. Widzisz, korzystając z matematyki, obliczasz pole i w rezultacie określasz, ile sadzonek zmieścisz w swojej zielonej oazie!
Przydatność w architekturze i budownictwie
Myśląc o architekturze, dostrzegamy pole do popisu dla geometrii. Gdy architekt przystępuje do projektowania nowego domu, w pierwszej kolejności oblicza pole dachu w kształcie trójkąta, aby oszacować ilość materiału potrzebnego na pokrycie. Ponadto, przy okazji może też obliczyć, ile deszczówki da się zebrać. W związku z tym obliczenia pola trójkąta sprawiają, że budynki stają się nie tylko estetyczne, ale również funkcjonalne. Można to określić jako sztukę matematyki zastosowanej w praktyce!
Uroki codziennego życia
Teraz wyobraź sobie, że organizujesz grilla. Zaczynasz układać stół, krzesła oraz grill. Pragniesz wyznaczyć pole swojej „grillowej strefy”, aby upewnić się, że wszystko się zmieści i nie narobisz bałaganu u sąsiadów – bo w końcu to nie jest mile widziane! Wykorzystując wzór na pole trójkąta, obliczasz, ile miejsca potrzebujesz na rozłożenie wszystkich swoich gastronomicznych skarbów. Dzięki temu Twoje spotkanie w ogrodzie staje się nie tylko smakowite, ale także wygodne!
Jak widzisz, obliczanie pola trójkąta to nie tylko nudne lekcje matematyki w szkole! To praktyczna umiejętność, która może uratować Cię przed chaosem w codziennym życiu, a przy okazji uczynić Cię bohaterem w oczach przyjaciół. Dlatego następnym razem, gdy będziesz miał do czynienia z wyzwaniem, które wymaga odrobiny matematyki, pamiętaj, że pole trójkąta czeka gdzieś w pobliżu, gotowe, by pomóc Ci w rozwiązaniu problemu!
Najczęstsze błędy podczas obliczania pola trójkąta i jak ich unikać
Obliczanie pola trójkąta może wydawać się proste jak bułka z masłem, jednak często z pozoru łatwe zadania potrafią nas zaskoczyć. Najczęstsze błędy, jakie popełniamy przy obliczaniu pola trójkąta, przypominają niezaproszone czynniki, które mogą przyjść w najmniej oczekiwanym momencie. Na przykład, zapominając o wysokości trójkąta, robimy coś podobnego do pieczenia ciasta bez mąki – niby robi się, ale efekt końcowy nie zachwyca. To wyobrażenie z pewnością rozweseli tych, którzy mylą narzędzia matematyczne, zwłaszcza gdy zamiast użyć wzoru z wysokością, zdecydują się na formułę na pole prostokąta. Dobrze, że matematyka nie ma serca, bo pewnie smuciłaby się na widok takich grzeszników!
Najpopularniejsze faux pas
Inny błąd, który łatwo popełnić, to wybór niewłaściwego wzoru. Weźmy przykład: próbując obliczyć pole trójkąta znając długości jego boków oraz kąt między nimi, możemy pomyśleć o wzorze, który wymaga wysokości. W takiej sytuacji duchy matematyki będą nas straszyć na każdej kartce z zadaniami! Dlatego warto mieć rozpisane formuły oraz wiedzieć, kiedy je zastosować, ponieważ korzystanie z niewłaściwego wzoru przypomina próbę otwarcia smakołyku w niezbyt odpowiedni sposób... unikajmy takich wpadek!
- Zapominanie o wysokości trójkąta
- Wybór niewłaściwego wzoru
- Mieszanie narzędzi matematycznych
Przykład błędnych kroków
Gdy pracujemy z bokami trójkąta a, b i c, nie zapominajmy o koncepcji połowy obwodu, czyli „p”!
Bez tego nasza przygoda z wzorem Herona będzie niepełna i ograniczy naszą wyobraźnię matematyczną.
Dlatego postaraj się być jak najlepiej zorganizowanym uczniem i zapisuj wszystkie niezbędne dane! W końcu lepiej mieć pod ręką przypomnienie, kto, gdzie i co wymyślił, niż błądzić jak zgubiony w lesie jeleń, zastanawiając się, gdzie popełniliśmy błąd!
Na koniec pamiętajmy, że praktyka czyni mistrza. Im więcej zadań rozwiążemy, tym mniej tych matematycznych pułapek potrafi nas zaskoczyć. Protip: nie oczekuj od siebie perfekcji od razu – każdy wielki matematyk miał zapewne na koncie dziesiątki niewłaściwych obliczeń, a mimo to wciąż odkrywał nowe tajemnice świata liczb!
| Błąd | Opis |
|---|---|
| Zapominanie o wysokości trójkąta | Nie uwzględnienie wysokości trójkąta przy obliczeniach prowadzi do błędnych rezultatów. |
| Wybór niewłaściwego wzoru | Stosowanie wzorów, które nie pasują do dostępnych danych, takich jak długości boków i kąt. |
| Mieszanie narzędzi matematycznych | Używanie formuł lub podejść, które nie są adekwatne do problemu, np. wzór na pole prostokąta zamiast trójkąta. |