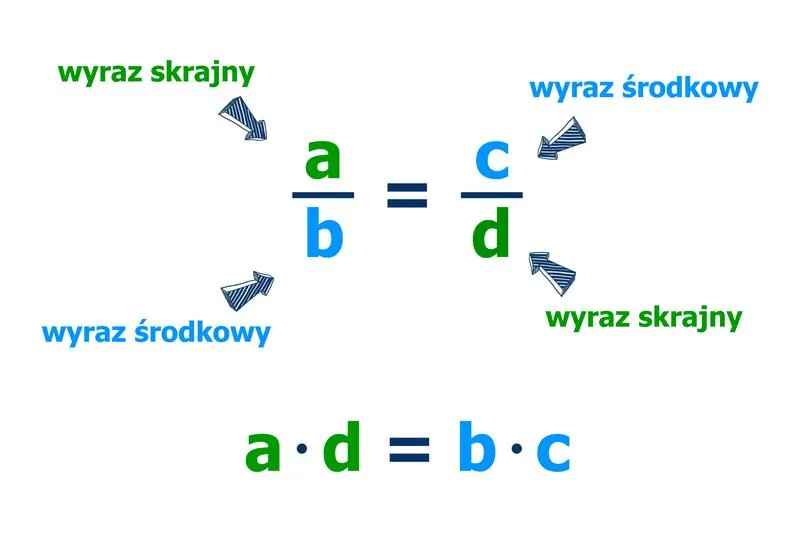
Zrozumienie proporcji stanowi klucz do osiągnięcia sukcesu w matematyce, co otwiera drzwi do szerszych możliwości w nauce. Proporcje można w uproszczeniu porównać do relacji między dwoma wielkościami, które zmieniają się w równym stosunku. Na przykład, jeśli a wynosi 2, a b to 4, to proporcja między nimi wynosi 1:2. Proste? Owszem! Jednak, gdy przychodzi co do czego i trzeba zastosować te matematyczne koncepcje w rzeczywistych zadaniach tekstowych, sytuacja potrafi przysporzyć nieco zmartwień. Przecież, kto by pomyślał, że takie dwa obiekty jak jabłko i pomarańcza mogą mieć wspólny mianownik? Tutaj matematyka zyskuje kosmiczną moc!
- Proporcje w matematyce są relacjami między dwiema wielkościami zmieniającymi się w równym stosunku.
- Wyróżniamy dwa typy proporcji: prostą, gdy obie wartości rosną lub maleją w tym samym kierunku, oraz odwrotną, gdy jedna rośnie, a druga maleje.
- Proporcje mają wiele praktycznych zastosowań w codziennym życiu, takich jak zakupy, gotowanie czy planowanie czasu.
- Umiejętność rozpoznawania typów proporcji ułatwia rozwiązywanie zadań matematycznych.
- Rozwiązywanie zadań z proporcjami można porównać do gotowania – wymaga zrozumienia i dokładności.
- Proporcje mają długą historię, sięgającą starożytnych cywilizacji, wpływając na różne dziedziny, takie jak architektura i sztuka.
- Nauka o proporcjach łączy matematykę z praktycznymi umiejętnościami, czyniąc ją przyjemnością, a nie tylko wyzwaniem.

Wyróżniamy dwie główne kategorie proporcji: prostą oraz odwrotną. Proporcja prosta występuje w sytuacji, gdy obie wartości rosną lub maleją w tym samym stosunku. Na przykład, gdy 4 kilogramy jabłek kosztują 8 złotych, wówczas 8 kilogramów kosztuje 16 złotych – proste jak drut! Natomiast proporcja odwrotna pojawia się w momencie, gdy jedna wartość rośnie, a druga maleje. Wyobraź sobie grupę ludzi, którzy próbują podzielić pizzę. Im więcej osób, tym mniej kawałków przypada na jednego z nich. Tak działa odwrócona proporcja! Widać, że matematyka staje się nie tylko interesująca, ale i... smakowita!
Proporcje w życiu codziennym
Nie można zapominać, że wokół nas znajdziemy mnóstwo przykładów zastosowania proporcji. W każdej chwili, niezależnie od tego, czy robimy zakupy, gotujemy, czy planujemy podróż, w miarę wzrostu jednej wartości, inna również musi się dostosować. Proporcje przypominają matczyny instynkt – zawsze odnajdują dla siebie miejsce w danej sytuacji. Przy analizie zadań tekstowych dotyczących zjawisk i sytuacji z codziennego życia, warto odważyć się wyjść poza liczby i dostrzec prawdziwe relacje. Nawet jeśli czasami wymaga to większego skupienia, prowokuje nas do logicznego myślenia oraz zrozumienia dynamiki różnych zjawisk.

Kluczowe staje się również umiejętne rozpoznawanie typów proporcji. Wiedza o tym, czy mamy do czynienia z proporcją prostą czy odwrotną, umożliwia właściwe podejście do rozwiązywania zadań. Zasada jest prosta: gdy obie wielkości zmieniają się w tym samym kierunku, mamy do czynienia z proporcją prostą. Natomiast, jeśli jedna rośnie, a druga maleje – to znak, że czas na odwrotną! Ucz się, analizuj, ćwicz, a zauważysz, jak z czystej matematyki staje się ona prawdziwą przyjemnością, a proporcje przestają być jedynie matematycznym wyzwaniem i zaczynają przypominać uporządkowaną grę w liczenie!
Praktyczne zastosowania proporcji w codziennym życiu
Proporcje stanowią niezastąpione narzędzie, które przy odpowiednim wykorzystaniu znacząco ułatwia nasze codzienne życie. Wyobraź sobie sytuację, gdy wybierasz się na zakupy spożywcze. Stoisz przed półką z makaronem, a cena paczki ważącej zaledwie kilka gramów okazuje się dość wysoka. W tej chwili szybka kalkulacja może uratować Twój budżet! Wystarczy, że porównasz, ile makaronu otrzymujesz za daną cenę, zestawiając ją z ceną większych opakowań. Dzięki temu przyznasz sobie nie tylko oszczędności, ale także poczucie satysfakcji z dobrze podjętej decyzji. Zobacz, jak kilka prostych obliczeń może przekształcić Twoje zakupy w emocjonującą przygodę oszczędnościową!
Innym rewelacyjnym przykładem wykorzystania proporcji są kulinarne eksperymenty. Z pewnością każdy, kto próbował piec ciasto bez odpowiedniej receptury, wie, że proporcje składników są kluczowe. Jeśli masz przepis na pyszne brownie przeznaczone dla małego wojska, a w swojej kuchni posiadasz jedynie garść ciasteczek, nie ma powodu do zmartwień! Wystarczy, że proporcjonalnie zmniejszysz ilości składników, a Twoje delikatne wypieki będą wręcz idealne na mały lunch! Dzięki umiejętnemu stosowaniu proporcji stajesz się prawdziwym mistrzem kuchni, który potrafi dostosować smak do różnych okazji — niezależnie od tego, czy organizujesz urodzinowe przyjęcie, czy kameralną kolację przy świecach!
Proporcje w planowaniu czasu
Może to brzmieć zaskakująco, lecz proporcje znakomicie sprawdzają się również w planowaniu czasu. Przeprowadźmy mały eksperyment — załóżmy, że zamierzasz spędzić pół dnia w parku i chcesz maksymalnie wykorzystać ten czas. Mierzysz, ile czasu potrzebujesz na dotarcie do parku oraz jak długo zamierzasz przeskakiwać z jednej atrakcji do drugiej. Dzięki proporcjom ustalisz, ile czasu przypiszesz konkretnym aktywnościom, aby wszystko zgrało się w idealny sposób!
Zaskoczony? Okazuje się, że proporcje mogą uratować Twoje dni przed chaosem i zamieszaniem. Poświęć chwilę na przemyślenie, ile czasu będzie potrzebne na jedzenie, spacer czy relaks na trawie z książką — wszystko to możesz zorganizować tak, aby spokojnie cieszyć się każdą chwilą. Obliczając proporcje, zyskujesz nie tylko czas, ale także spokój ducha.
Przy planowaniu czasu w parku możesz uwzględnić następujące aktywności:
- czas na dojazd do parku
- czas na jedzenie piknikowe
- czas na zwiedzanie atrakcji
- czas na relaks i czytanie książki
- czas na powrót do domu
Jak rozwiązywać zadania z proporcjami: Krok po kroku
Rozwiązywanie zadań z proporcjami przypomina gotowanie – początkowo może wydawać się skomplikowane, ale z czasem staje się naprawdę przyjemne! Gdy zaczynasz zadanie, pierwszym krokiem staje się dokładne zapoznanie się z treścią. Zamiast koncentrować się wyłącznie na liczbach, spróbuj wyłowić kluczowe informacje, bo to one będą niczym przepisy w kuchni, prowadzące cię do smaku sukcesu. Zapisz posiadane dane oraz określ niewiadomą. Pamiętaj, że ta niewiadoma odpowiada na pytanie postawione w zadaniu. Jeśli dobrze ją wytypujesz, już połowa sukcesu znajduje się po twojej stronie!
Następnie, gdy zidentyfikujesz swoje dane, przyjrzyj się zależnościom między nimi. Czy rosną jednocześnie, czy może jedno maleje, kiedy drugie wzrasta? To pytanie pomoże ci w wyborze odpowiedniej proporcji. Kiedy obie wielkości idą w parze, zyskujesz proporcję prostą. W przeciwnym przypadku mówimy o proporcji odwrotnej. Niech te proporcje będą twoimi sprzymierzeńcami, niczym dobrze dobrana para taneczna na parkiecie matematyki!
Etapy rozwiązywania zadań z proporcjami: kluczowe kroki
Teraz nadszedł moment na ułożenie równania! Zapisz proporcję, a następnie przekształć ją, by wyizolować niewiadomą. Pamiętaj, że chronologiczny porządek podczas zapisywania proporcji ma ogromne znaczenie – bądź jak skrupulatny szef kuchni, który zawsze ma wszystkie składniki dokładnie wyważone! Kiedy już obliczysz wynik, wróć do treści zadania, aby upewnić się, że naprawdę odpowiada na postawione pytanie. Świetny wynik stanie się nagrodą za twoją ciężką pracę oraz dokładność!
Na koniec, pamiętaj, że praktyka czyni mistrza! Im więcej zadań z proporcjami rozwiążesz, tym bardziej intuicyjnie podchodzisz do nowych wyzwań. Wykorzystuj różnorodne przykłady z życia codziennego – od obliczeń w sklepie po planowanie czasu na ważne wydarzenia. Dzięki temu matematyka stanie się dla ciebie nie tylko nauką, ale także przyjemnością, a proporcje przestaną być groźnym przeciwnikiem, stając się twoim najlepszym przyjacielem w świecie liczb!
| Krok | Opis |
|---|---|
| 1 | Dokładne zapoznanie się z treścią zadania i wyłowienie kluczowych informacji. |
| 2 | Zapisanie posiadanych danych oraz określenie niewiadomej odpowiadającej na pytanie. |
| 3 | Przyjrzenie się zależnościom między danymi (czy rosną jednocześnie, czy jedno maleje?). |
| 4 | Wybór odpowiedniej proporcji (prosta lub odwrotna) na podstawie zauważonych zależności. |
| 5 | Ułożenie równania i zapisanie proporcji, dbając o chronologiczny porządek danych. |
| 6 | Obliczenie wyniku i powrót do treści zadania, aby sprawdzić poprawność odpowiedzi. |
| 7 | Regularna praktyka oraz rozwiązywanie różnorodnych zadań z proporcjami, aby zyskać intuicję. |
Czy wiesz, że proporcje były znane i stosowane już w starożytności? Egipcjanie posługiwali się nimi, aby obliczać powierzchnie pól uprawnych, a ich umiejętność w obliczeniach była na tyle zaawansowana, że potrafili też tworzyć skomplikowane systemy miar!
Ciekawe przykłady z historii matematyki dotyczące proporcji
W historii matematyki proporcje odgrywały naprawdę ważną rolę, ponieważ ich istnienie sięga aż do starożytnych cywilizacji. Greccy matematycy, tacy jak Pitagoras czy Euklides, wykorzystywali je, by odkrywać tajemnice otaczającego ich świata. Wyobraźcie sobie szaloną ucztę, gdzie każdy uczony, dzierżąc tablicę i woskowy tablet, rozważa, jak dodanie kolejnej oliwki wpływa na ogólną ilość przekąsek! No cóż, nie tylko oliwki grały kluczową rolę w tych obliczeniach, lecz przede wszystkim zrozumienie, że proporcje łączą różne wielkości, przypominało im o harmonii w naturze.
Skupiając się na starożytnym Egipcie, zauważamy, że tamtejsi matematycy także mieli sporo do powiedzenia w tej kwestii. Intervaliści, czyli egipscy liczydłarze, wykorzystywali proporcje w praktyce budowlanej. Dzięki nim potrafili nadzwyczaj precyzyjnie obliczać, ile kamieni potrzeba do zbudowania wielkich piramid. Gdyby tylko mogli zamówić kamienie z dostawą do domu na aplikacji, oszczędziliby mnóstwo czasu. Musieli jednak polegać na proporcjach, które czasami przyprawiały ich o ból głowy bardziej niż nieprzyjemny posiłek.
Praktyczne zastosowania proporcji w średniowieczu
W średniowieczu proporcje zajmowały równie istotne miejsce w naukach przyrodniczych oraz inżynierii. Na przykład architekci katedr stosowali proporcje do ustalenia idealnych rozmiarów okien, by światło wpadało w najpiękniejszy sposób. Kiedy pleban wznosił katedrę, zrozumienie, że większe okna wiążą się z większymi proporcjami świętości, musiało przynieść efekt „WOW”. Jak można myśleć o średniowiecznym budownictwie bez tej cudownej idei, że wszystko można zharmonizować za pomocą złotego podziału? To właśnie te proporcje najpierw przeniosły ideę estetyki, a następnie, jak pokazuje historia sztuki, każdy artysta w późniejszych wiekach mógł odnaleźć się w tej samej matrycy.
Proporcje w matematyce przetrwały stulecia, a ich zastosowanie przekształcało się na różne sposoby. Ludzie dowiedli, że nie istnieją rzeczy niemożliwe, gdy chodzi o obliczenie najbardziej skomplikowanych wartości matematycznych. Współczesna matematyka oraz nauki ścisłe korzystają z tego cennych dziedzictwa. Każdy uczeń, zmagając się z proporcjami w zadaniach tekstowych, musi zrozumieć, że liczenie to nie tylko nudne wykonywanie obliczeń, ale także odkrywanie fascynujących powiązań w otaczającym nas świecie. Proporcje zatem to nie tylko matematyka, lecz prawdziwa historia, która wciąż trwa!
Poniżej przedstawiam kilka przykładów zastosowań proporcji w różnych dziedzinach:
- Architektura - idealne proporcje okien w katedrach
- Sztuka - wykorzystanie złotego podziału w kompozycjach malarskich
- Matematyka - obliczenia w geometrze i analizie matematycznej
- Inżynieria - obliczenia potrzebnych materiałów w budownictwie
Źródła:
- https://www.polecanekorepetycje.pl/zadania-tekstowe-z-proporcji-i-rownan-2/
- https://szkolazklasa20.pl/twierdzenie-talesa-na-praktycznych-przykladach-definicja-i-wzory/