Dowodzenie matematyczne nie jest jedynie sztuką, ale przypomina również alchemię logiczną! W matematycznym świecie, gdzie liczby i figury geometryczne przenikają się nawzajem, dysponujemy kilkoma potężnymi narzędziami. Indukcja matematyczna stanowi jedno z tych narzędzi; opiera się na zasadzie, że „jeśli działa dla małego, to działa dla dużego”. To przypomina trochę film „Terminator” – jeśli mały robot przetrwał, to duży też poradzi sobie! Indukcja umożliwia udowodnienie twierdzeń dla całej nieskończonej rodziny liczb naturalnych, zaczynając od solidnych fundamentów, czyli od najmniejszych liczb.
- Dowodzenie matematyczne jest kluczowym narzędziem w matematyce, przypominającym alchemię logiczną.
- Indukcja matematyczna działa na zasadzie wykazywania prawdziwości twierdzenia dla większych liczb na podstawie dowodu dla liczby mniejszej.
- Indukcja składa się z dwóch kluczowych kroków: bazy indukcyjnej i kroku indukcyjnego.
- Inne metody dowodzenia to dowód przez sprzeczność oraz stosowanie kontrprzykładów.
- Indukcja ma zastosowania w różnych dziedzinach matematyki, od teorii liczb po geometrię.
- Umiejętność dowodzenia jest niezbędna w rozwiązywaniu problemów, analizie algorytmów i badaniu struktur danych.
- Praktyka i systematyczne podejście są kluczowe dla rozwijania umiejętności dowodzenia matematycznego.
- Indukcję można zastosować w codziennym życiu do analizowania trendów oraz przewidywania sukcesów w różnych dziedzinach.
Warto zwrócić uwagę, że indukcja matematyczna składa się z dwóch kluczowych kroków: bazy indukcyjnej oraz kroku indukcyjnego. W bazie, jak na szkolnej lekcji, nie ma sensu się oszukiwać; musimy wykazać, że nasze twierdzenie jest prawdziwe dla najsłabszej jednostki, zazwyczaj dla liczby 1. Gdy baza okaże się mocna jak superbohater, przechodzimy do kroku indukcyjnego. W tym kroku zakładamy, że hipoteza działa dla pewnej liczby n, a następnie udowadniamy, że działa także dla n + 1. I voilà! Mamy dowód, a nasze zjawiskowe kroki prowadzą nas po krawędzi matematycznego przepaści!
Inne formy dowodzenia w matematyce
W matematyce oprócz indukcji występuje jeszcze kilka różnych podejść do dowodzenia, na przykład dowód przez sprzeczność. To nic innego jak wersja matematycznego „CSI”. Przyjmujemy za prawdziwe, że coś jest fałszywe, a następnie śledzimy tropy prowadzące do nieuchronnej katastrofy – sprzeczności. Jeśli dostrzegamy, że coś w całym układzie jest niezgodne, automatycznie stwierdzamy, że nasze pierwotne założenie było mylne. Również kontrprzykłady mogą zaskakiwać niczym nieprzewidziane „twisty” w ulubionych serialach; ludzie myślą, że mają rację, a tu bum – mylą się!
Na zakończenie, gdy poczujesz się zagubiony w świecie dowodzenia, pamiętaj, że w matematyce nie jesteś sam! Każda metoda dowodzenia to instrument w orkiestrze matematycznej – każda z nich ma swoje unikalne brzmienie i znaczenie. Dostosuj odpowiednią metodę do zagadnienia, a matematyczne melodie będą płynąć gładko jak po maśle. I pamiętaj: praktyka czyni mistrza, więc ćwicz swoje dowody, aż staniesz się matematycznym ninja!
| Metoda dowodzenia | Opis | Kluczowe kroki |
|---|---|---|
| Indukcja matematyczna | Dowodzenie, które wykazuje, że jeśli twierdzenie jest prawdziwe dla małej liczby, to jest prawdziwe także dla większych. | Baza indukcyjna, krok indukcyjny (zakładam, że działa dla n, dowodzę dla n + 1). |
| Dowód przez sprzeczność | Przyjmowanie fałszywego za prawdziwe i prowadzenie do sprzeczności, co dowodzi, że pierwotne założenie było mylne. | Założenie fałszywego, prowadzenie do sprzeczności. |
| Kontrprzykłady | Dowodzenie, które zaskakuje poprzez wykazanie, że twierdzenie jest fałszywe przez podanie konkretnego przykładu. | Znalezienie przykładu, który przeczy założeniu. |
Praktyczne przykłady dowodzenia: Zastosowanie w rozwiązywaniu problemów
Indukcja matematyczna, mimo że brzmi jak magiczne zaklęcie, stanowi jedno z najważniejszych narzędzi w matematyce. Możesz myśleć o niej jako o mostku, który łączy różne punkty, wskazujące na prawdziwość dowodów. Dzięki tej metodzie potwierdzamy, że pewne stwierdzenia są prawdziwe dla nieskończonej liczby przypadków, opierając się na dwóch krokach: bazowej indukcji oraz kroku indukcyjnego. Na początek jednak musisz zrozumieć, jak zastosować tę metodę – a więc, jak poprowadzić nasze matematyczne łódki po wzburzonych wodach logicznych argumentów!
Praktyczne przykłady indukcji – od teorii do praktyki
Wyobraź sobie, że chcesz udowodnić, iż suma pierwszych n liczb naturalnych (1 + 2 + ... + n) daje wynik równy n(n + 1)/2. Zaczynasz od bazy indukcji, sprawdzając, czy stwierdzenie działa dla n = 1. Rzeczywiście się zgadza, bo 1 = 1(1 + 1)/2. Następnie przechodzisz do kroku indukcyjnego. Zakładasz, że twoja teza jest prawdziwa dla k, a następnie udowadniasz, że działa także dla k + 1. Składając wszystkie liczby niczym klocki Lego, dostrzegasz, że matematyczne budowle w końcu się łączą! Prosta logika, ale warto ją wyłożyć na stół, aby cieszyć się pełnią matematycznego życia!
Indukcja okazuje się również nieoceniona w dziedzinie informatyki. Wyobraź sobie proces projektowania rekurencyjnego algorytmu. Jak udowodnisz, że działa poprawnie? Dokładnie w ten sposób – stosując indukcję! Możesz śledzić poprawność algorytmu krok po kroku, budując zaufanie do swojej konstrukcji niczym rycerz ze rozwiniętym sztandarem. Przy odpowiedniej strukturze dowodu potrafisz zaimponować swoim kolegom programistom, którzy z pewnością wpadną w podziw, ponieważ podążając tą drogą, nie tylko osiągasz sukces, ale i doświadczasz satysfakcji matematycznej!
Indukcja w codziennym życiu – nie tylko teoretycznie!
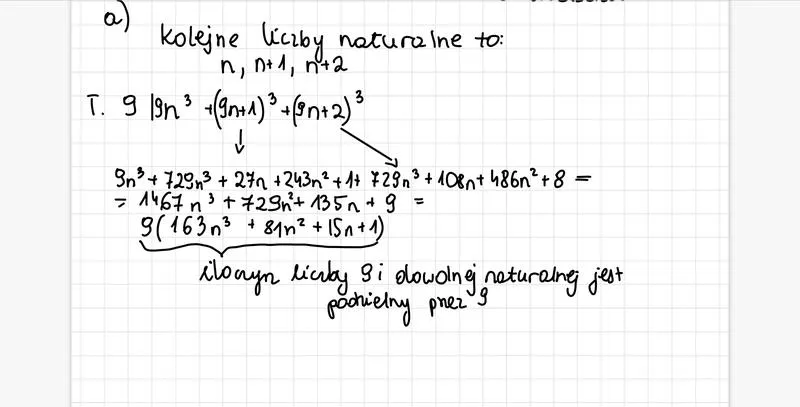
Zastanówmy się, jak można wykorzystać tę metodę w codziennym życiu. Okazuje się, że zasady indukcji można skutecznie zastosować do rozwiązywania problemów rzeczywistego świata! Od przewidywania sukcesów inwestycji po analizowanie trendów w mediach społecznościowych – wszystko to można potwierdzić w sposób przypominający matematyczną indukcję. Zaczynając od podstawy, w której stwierdzenie jest prawdziwe, możesz dążyć do analizowania większych zestawów danych, budując pewność krok po kroku. Widać zatem, że indukcja nie kończy się w klasie matematycznej, lecz otwiera się jak książka z nowymi przygodami w przestrzeni życia!
Poniżej przedstawiam kilka obszarów, w których indukcja może być zastosowana w codziennym życiu:
- Przewidywanie sukcesów inwestycji na podstawie wcześniejszych wyników
- Analiza trendów w mediach społecznościowych na podstawie obserwowanych danych
- Rozwiązywanie problemów logistycznych w codziennych zadaniach
- Ustalanie reguł w grach na podstawie wcześniejszych ruchów
Rola dowodzenia w różnych dziedzinach matematyki: Od teorii liczb po geometrię
Dowodzenie w matematyce stanowi prawdziwą magię, która przekształca chaotyczne zbiory liczb i figur w eleganckie twierdzenia. Różne dziedziny matematyki, począwszy od teorii liczb, a skończywszy na geometrii, wykorzystują dowody w zróżnicowany sposób. Jednak jedno pozostaje niezmienne – siła logiki oraz zrozumienia. Na przykład w teorii liczb dowody przez indukcję działają jak klucz, otwierający drzwi do nieskończonych możliwości. Umożliwiają one udowadnianie stwierdzeń dotyczących wszelkich liczb naturalnych, nadając jednocześnie matematycznym twierdzeniom elegancję oraz porządek.
Natomiast w geometrii dowody przybierają bardziej wizualną i przestrzenną postać. W tym kontekście wykorzystujemy dowody, które trudno zobrazować jedynie za pomocą cyfr. Na przykład możemy przywołać znane twierdzenie mówiące, że suma kątów wewnętrznych w wielokącie o n bokach wynosi (n-2) * 180°. Taki dowód nie tylko poszerza nasze zrozumienie kształtów, ale również zachęca do myślenia przestrzennego, które w matematyce odgrywa kluczową rolę. Zresztą, czy geometryczne figury nie fascynują swoim niepowtarzalnym urokiem?
Indukcja i geometria – połączenie, które działa

Indukcja w geometrii to prawdziwe dzieło sztuki. Ta technika dowodzenia pozwala na potwierdzanie twierdzeń dotyczących nie tylko kątów i długości, ale także skomplikowanych zależności pomiędzy różnymi figurami. Istnieje wiele przykładów, a każdy z nich może prowadzić do fascynujących odkryć. Jeśli chwilę się nad tym zastanowimy, zauważymy, że każdy dowód w geometrii przypomina misternie utkany gobelin – z każdego wątku wynika coś większego, a całość staje się swoistym dziełem sztuki matematycznej. Co więcej, ukazanie tej metody młodszym pokoleniom ma nieocenioną wartość – wprowadza ich do królestwa logiki oraz kreatywności.
W końcu, zarówno w teorii liczb, jak i w geometrii, dostrzegamy, że dowodzenie nie tylko ułatwia zrozumienie złożonych koncepcji matematycznych, ale także rozwija umiejętność myślenia analitycznego. Zatem, przy wszystkich tych złożonych dowodach, możemy śmiało stwierdzić, że matematyka to nie tylko nauka – to prawdziwe artystyczne przedsięwzięcie, gdzie każdy dowód stanowi małe arcydzieło logiczne. Dlatego warto zgłębiać zarówno teoretyczne, jak i praktyczne aspekty dowodzenia, aby odkryć nie tylko moc matematyki, ale także radość płynącą z jej nauki.
Jak rozwijać umiejętności dowodzenia: Rady dla studentów i pasjonatów matematyki
Rozwój umiejętności w zakresie dowodzenia matematycznego stanowi nie lada wyzwanie. Dlatego studenci oraz pasjonaci tej dziedziny często odczuwają frustrację. Warto jednak zauważyć, że kluczem do osiągnięcia sukcesu staje się systematyczne podejście. Dzięki niemu można krok po kroku opanować tajniki dowodzenia. Na początek, dobrze jest skupić się na jednej z najpotężniejszych metod matematycznych, czyli indukcji matematycznej. Choć ta metoda wydaje się skomplikowana, to przy właściwym użyciu potrafi otworzyć przed nami nowe horyzonty logicznego myślenia!
Zanim przystąpimy do praktyki, musimy zrozumieć, czym dokładnie jest indukcja matematyczna. Każdy dowód indukcyjny dzieli się na dwa kluczowe etapy: bazę indukcyjną oraz krok indukcyjny. Zaczynamy od udowodnienia prawdziwości stwierdzenia dla najmniejszej liczby naturalnej, którą najczęściej stanowi liczba jeden. Następnie, w kroku indukcyjnym zakładamy, że dane twierdzenie jest prawdziwe dla liczby k i udowadniamy, że również musi być prawdziwe dla k + 1. Warto porównać indukcję do wspinaczki: rozpoczynamy od jednego ciekawego szczytu, a z każdym krokiem odkrywamy nowe, wyższe partie!
Indukcja w praktyce: zalety i zastosowania
Indukcja matematyczna nie tylko ułatwia zrozumienie poszczególnych twierdzeń w mikroskali, ale również sprawdza się w bardziej złożonych problemach takich jak analiza algorytmów czy badanie struktur danych. Dzięki indukcji możemy udowadniać różnorodne własności liczb naturalnych oraz szeregów arytmetycznych. Kiedy nauczysz się skutecznie wykorzystywać dowody oparte na indukcji, nie tylko zwiększysz pewność siebie, ale także wyniesiesz swoje umiejętności analityczne na wyższy poziom! A kto nie chciałby odnosić sukcesów w matematycznej dżungli i rozwiązywać nawet najbardziej złożonych problemów z uśmiechem na twarzy?
- Umożliwia zrozumienie i udowodnienie własności liczb naturalnych.
- Pomaga w analizie algorytmów.
- Stosowana w badaniu struktur danych.
- Ułatwia potwierdzanie hipotez w matematyce.
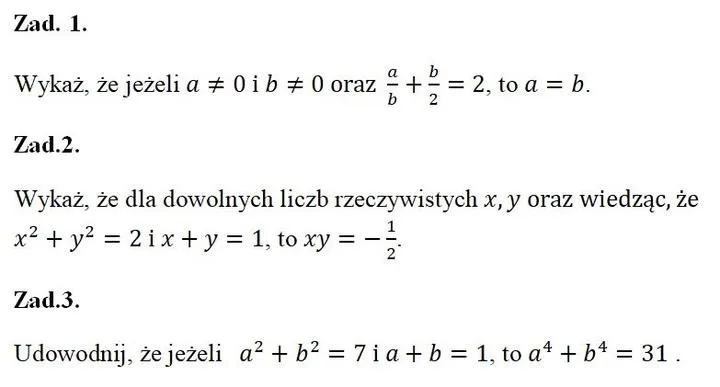
Nie zapominaj, że klucz do osiągnięcia sukcesu kryje się w codziennej praktyce. Regularne ćwiczenie dowodów indukcyjnych, rozwiązywanie problemów oraz omawianie ich z innymi entuzjastami matematyki sprawią, że z czasem staną się one dla ciebie intuicyjne i przyjemne. Nie obawiaj się popełniać błędów – każda pomyłka to jedynie krok w kierunku głębszego zrozumienia. W końcu w matematyce, podobnie jak w życiu, błędy mają na celu naukę, a każdy rozwój to z pewnością coś, co warto świętować!
Źródła:
- https://www.zsnienowice.pl/dowody-przez-indukcje-przyklady-i-cwiczenia