Trójkąt to figura geometryczna, która pełna jest tajemnic, przypominając wróżkę w matematyce! Aby dobrze zrozumieć, co wpływa na pole trójkąta, warto przyjrzeć się kilku podstawowym elementom tego kształtu. Najważniejszymi z nich są długości boków oraz wysokość. Najprostszy sposób na obliczenie pola trójkąta to zastosowanie wzoru: P = 1/2 * a * h, gdzie „a” oznacza długość boku, a „h” to wysokość opuszczona na ten bok. Właśnie w tym momencie czarująca magia geometrii zaczyna działać – wysoka wysokość sprawia, że pole rośnie, natomiast krótki bok to jak poszukiwanie skarbu w zaroślach – trudne, ale warte zachodu!
- Trójkąt to figura geometryczna, której pole można obliczyć na różne sposoby.
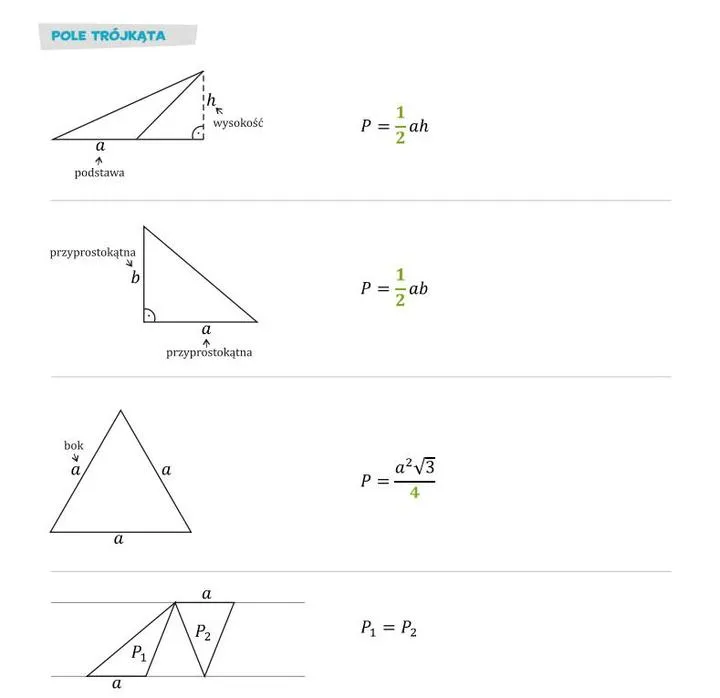
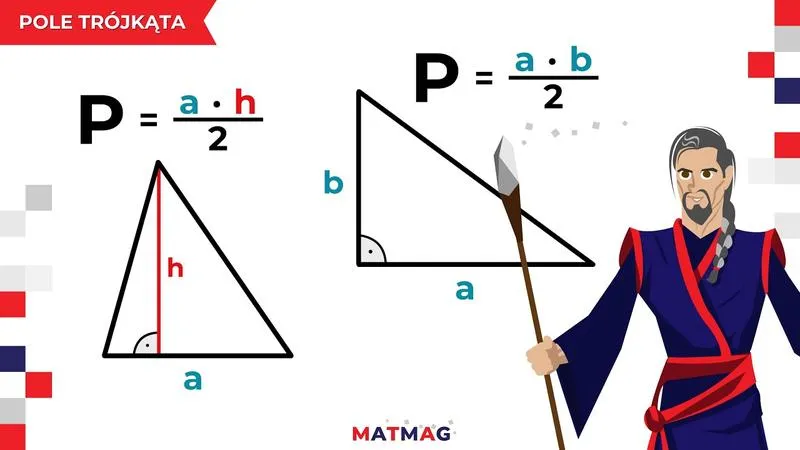
- Najprostszy wzór na pole trójkąta to P = 1/2 * a * h, gdzie a to długość podstawy, a h to wysokość.
- W przypadku trójkąta prostokątnego można zastosować wzór P = 1/2 * a * b, gdzie a i b to przyprostokątne.
- Dla trójkąta równobocznego używa się wzoru P = (√3/4) * a², gdzie a to długość boku.
- Wzór Herona P = √[s(s-a)(s-b)(s-c)] pozwala obliczać pole tylko na podstawie długości wszystkich boków.
- Dzięki funkcji sinus można obliczyć pole trójkąta znając długości dwóch boków i kąt między nimi: P = 1/2 * a * b * sin(C).
- Wzory na pole trójkąta mają zastosowanie nie tylko w matematyce, ale także w inżynierii, architekturze i innych dziedzinach.
- Alternatywne metody obliczania pola obejmują wykorzystanie promieni okręgów opisanych i wpisanych.
Niemniej jednak, nie tylko wysokość i podstawa definiują trójkąt! W bardziej skomplikowanych przypadkach korzystamy także z innych wzorów. Na przykład, kiedy znamy długości dwóch boków oraz kąt między nimi, możemy zastosować wzór: P = 1/2 * a * b * sin(γ). Tak, tak, sinus nie jest jedynie zagadkową funkcją, lecz sprytnym narzędziem w rękach matematyków! Dzięki temu narzędziu pole trójkąta zamienia się z nudnej cyfry w niezwykłe przeżycie, dając wszechstronną moc w obliczeniach.
Jak wybrać odpowiedni wzór do obliczeń?
Pole trójkąta można obliczać na kilka sposobów, a dokonanie najlepszego wyboru zależy od dostępnych danych. Gdy znasz wszystkie długości boków, wzór Herona sprawdzi się doskonale: P = √[p(p-a)(p-b)(p-c)], gdzie „p” oznacza połowę obwodu. Używając wzoru Herona, nie trzeba martwić się o wysokość, co przypomina ułatwiający życie przepis na tort! Jak mówi stare przysłowie: „triangulacja to klucz do sukcesu”, a wzór Herona stanowi najlepszego przyjaciela każdej matematycznej przygody.
Na zakończenie, niezależnie od tego, czy masz do czynienia z ogromnym trójkątem budowlanym, czy z niewielkim trójkątem ukazującym ulubioną formę w twoim ogródku, znajomość tych podstawowych wzorów na pole pozwoli Ci stać się matematykiem znad poziomy! Dlatego pamiętaj – w każdym trójkącie kryje się nie jedna, a wiele tajemnic, które czekają na odkrycie przez odważnego matematyka!
Jak wykorzystać wzór na pole trójkąta w praktycznych zadaniach?
Wzór na pole trójkąta, mimo iż wydaje się prosty, w rzeczywistości potrafi rozwiązać wiele zagadek geometrycznych! Od momentu, gdy zaczynamy planować nasze ogrody, aż po budowę wymarzonego domu, wzór ten okazuje się niezwykle przydatny w codziennym życiu. Najpopularniejszym sposobem na obliczenie pola trójkąta pozostaje znane wszystkim równanie: pole = 1/2 * a * h, gdzie „a” oznacza podstawę, a „h” wysokość. Jednak kto powiedział, że musimy ograniczać się wyłącznie do jednego sposobu? Dzięki różnorodności wzorów możemy wykorzystać tę magię matematyki w różnych sytuacjach oraz z różnymi danymi! Sprawdźmy, jak to się sprawdza!
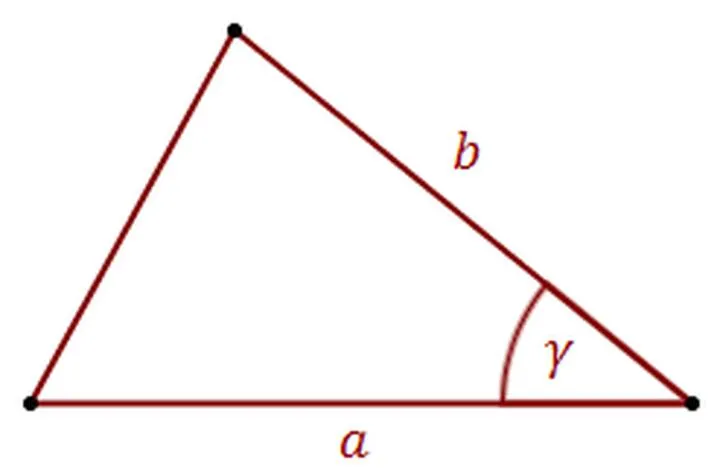
Wyobraźmy sobie sytuację, że planujemy mały ogródek w kształcie trójkąta. Dzięki wzorowi na pole trójkąta mamy możliwość oszacowania, ile ziemi potrzebujemy do jego obsadzenia. Nie ma prostszego sposobu na to! Gdy tylko znamy długość podstawy i wysokości, wystarczy podstawić wartości do wzoru, a wynik pojawi się natychmiast! A co, jeśli nie wiemy, jaka jest wysokość? Spokojnie! Możemy skorzystać z alternatywnych wzorów, na przykład, znając długości wszystkich boków, możemy sięgnąć po genialny wzór Herona, który sprawdzi się w każdej sytuacji!
Jak dobrać odpowiedni wzór?
Każdy typ trójkąta wymaga nieco innego podejścia. W przypadku trójkąta prostokątnego najlepiej zastosować prosty wzór pole = 1/2 * a * b, gdzie a i b stanowią przyprostokątne. Z kolei, gdy mamy do czynienia z trójkątem równobocznym, pole obliczamy, korzystając z formuły: P = (√3/4) * a²! Takie kombinacje przyczyniają się do tego, że każdy miłośnik matematyki może stać się ukrytym mistrzem geometrii. Co więcej, w przypadku nieprzewidzianych zmian, takich jak zmiana kątów, przydatna będzie formuła uwzględniająca sinusy kątów, co sprawia, że obliczenia stają się jeszcze bardziej dynamiczne!
Oto kilka różnych wzorów, które można zastosować w różnych rodzajach trójkątów:
- Trójkąt prostokątny: pole = 1/2 * a * b
- Trójkąt równoboczny: pole = (√3/4) * a²
- Wzór Herona: pole = √(s * (s - a) * (s - b) * (s - c)), gdzie s = (a + b + c) / 2
- Wzór z użyciem sinusów: pole = 1/2 * a * b * sin(C), gdzie C to kąt między bokami a i b
Nie zapominajmy, że wzory na pole trójkąta nie tylko wspierają obliczenia, ale także uczą nas lepszego zrozumienia kształtów, które nas otaczają. Przydają się nie tylko w matematyce, ale również w inżynierii, architekturze oraz wielu innych dziedzinach. Posiadając to narzędzie w ręku, poczujesz się jak prawdziwy geometra, gotowy na każdą geometryczną przygodę! Pamiętaj też, że każdy trójkąt jest inny, więc nie bój się eksperymentować z różnymi wzorami!
Przykłady zastosowania wzoru na pole trójkąta w różnych dziedzinach
Obliczanie pola trójkąta to temat, który często wywołuje dreszcze u wielu uczniów. Jednak nie ma powodu do obaw! Wzór na pole trójkąta jest tak uniwersalny, że można go zastosować w różnych aspektach życia codziennego. Na przykład, jeśli pracujesz jako architekt, możesz z powodzeniem wykorzystać ten wzór do obliczenia powierzchni dachu o kształcie trójkąta. Wystarczy tylko znać długości boków, a reszta to już matematyczne wyzwanie! Może obawiasz się, że zmiana kąta wprowadzi zamieszanie? To nic innego jak ciekawy dodatek, który sprawi, że stworzysz idealną przestrzeń na nowoczesne okna dachowe.
Co więcej, wzór na pole trójkąta przydaje się nie tylko w architekturze. Wyobraź sobie, że jesteś farmerem, który pragnie zaaranżować swoje pole uprawne. Kto powiedział, że musi ono mieć kształt okrągły lub kwadratowy? Trójkątne pola również są jak najbardziej możliwe! Dzięki wzorowi Herona łatwo obliczysz, jak dużo zboża pomieści się na działce o kształcie trójkąta, nawet bez zmartwień o wysokość. Wystarczy znać długości boków, a to w sumie nie powinno nastręczać kłopotów!
Jak można wykorzystać wzór Herona w różnych dziedzinach?
Niezwykłe właściwości wzoru Herona sprawiają, że staje się on narzędziem niezwykle przydatnym w geodezji. Kiedy znajdujesz się na terenach o złożonej, wielobocznej topografii, gdzie standardowe obliczenia pól działek mogą być skomplikowane, wystarczy określić długości boków trójkąta utworzonego przez punkty graniczne. Następnie wystarczy użyć wzoru na pole, a Twoje problemy znikają jak za dotknięciem czarodziejskiej różdżki, co przynosi spokój i satysfakcję. A gdy dodasz do tego, że wzór Herona znajduje również zastosowanie w sztukach plastycznych czy muzyce, nie sposób nie wykazać zachwytu! Wyobraź sobie, jak malujesz fantastyczne obrazy w kształcie trójkąta, mając pełną kontrolę nad ich powierzchnią! To nie tylko sztuka, ale i matematyka w Jednym — prawda, że to fascynujące?
Jakie alternatywne metody obliczania pola trójkąta warto znać?
Obliczanie pola trójkąta wydaje się prostym zadaniem. Wiele osób myśli, że wystarczy znać długość podstawy oraz wysokości, aby wszystko poszło gładko. Jednak rzeczywistość potrafi zaskoczyć! Gdy nie dysponujemy wysokością, warto skorzystać z alternatywnych metod. Na przykład, jeśli znamy długości dwóch boków oraz kąt między nimi, to możemy zastosować wzór: \( P = \frac{1}{2} ab \sin \gamma \). Dzięki temu z powodzeniem wprowadzimy trygonometrię do rozwiązywania geometrycznych problemów, a efektem końcowym będzie pole trójkąta, które nie wymaga mierzenia wysokości. Jak to często powtarzają, "gotowanie na ogniu, którego nie widać" może mieć swoje zalety!
Co też ma do powiedzenia wzór Herona?
Gdy zdecydujemy się odejść od klasycznych pomiarów, warto zwrócić uwagę na wzór Herona. Ten wzór działa jak magik w naszym zestawie narzędzi matematycznych. Dzięki niemu obliczymy pole trójkąta, mając jedynie długości boków. Formuła przedstawia się następująco: \( P = \sqrt{s(s-a)(s-b)(s-c)} \), gdzie \( s \) to połowa obwodu trójkąta. To doskonałe rozwiązanie, zwłaszcza gdy boki są znane, a wysokość umyka gdzieś w mrokach zapomnienia. Zresztą, kto nie lubi odrobiny energetyzującej inspiracji, jaką dostarcza matematyka?!
Nie możemy również zapomnieć o innej istotnej metodzie: korzystanie z promieni okręgów opisanych oraz wpisanych. Wzory takie jak \( P = \frac{abc}{4R} \) (gdzie \( R \) to promień okręgu opisanego) czy \( P = r \cdot \frac{a+b+c}{2} \) (gdzie \( r \) to promień okręgu wpisanego) otwierają przed nami nowe perspektywy. Taki mały promień a tyle możliwości obliczeniowych! Podsumowując, znajomość tych alternatywnych metod sprawia, że pozostajemy dobrze przygotowani na matematyczne wyzwania, które pojawiają się nagle jak nieprzyjemna burza w letni dzień.
Poniżej przedstawiam kilka informacji na temat alternatywnych sposobów obliczania pola trójkąta:
- Korzystanie z długości dwóch boków i kąta między nimi: \( P = \frac{1}{2} ab \sin \gamma \)
- Wykorzystanie wzoru Herona: \( P = \sqrt{s(s-a)(s-b)(s-c)} \), gdzie \( s \) to połowa obwodu trójkąta
- Obliczanie pola za pomocą promienia okręgu opisanego: \( P = \frac{abc}{4R} \)
- Obliczanie pola za pomocą promienia okręgu wpisanego: \( P = r \cdot \frac{a+b+c}{2} \)
| Metoda obliczania pola trójkąta | Wzór | Opis |
|---|---|---|
| Korzystanie z długości dwóch boków i kąta między nimi | P = (1/2) ab sin(γ) | Wymaga znajomości długości dwóch boków oraz kąta między nimi. |
| Wykorzystanie wzoru Herona | P = √[s(s-a)(s-b)(s-c)] | Oblicza pole trójkąta na podstawie długości wszystkich boków. s to połowa obwodu trójkąta. |
| Obliczanie pola za pomocą promienia okręgu opisanego | P = (abc) / (4R) | Wymaga znajomości długości boków oraz promienia okręgu opisanego. |
| Obliczanie pola za pomocą promienia okręgu wpisanego | P = r * (a+b+c) / 2 | Wymaga znajomości długości boków oraz promienia okręgu wpisanego. |
Źródła:
- https://www.matemaks.pl/wzory-na-pole-trojkata.html
- https://zpe.gov.pl/a/pole-trojkata/D1011a4cs
- https://szkolamaturzystow.pl/baza-wiedzy/1609694349-pole-trojkata
- https://npseo.pl/wzor-na-pole-trojkata/
- https://www.supermatma.pl/jak-obliczyc-pole-trojkata-ze-wzoru-herona
- https://www.omnicalculator.com/pl/matematyka/pole-trojkata