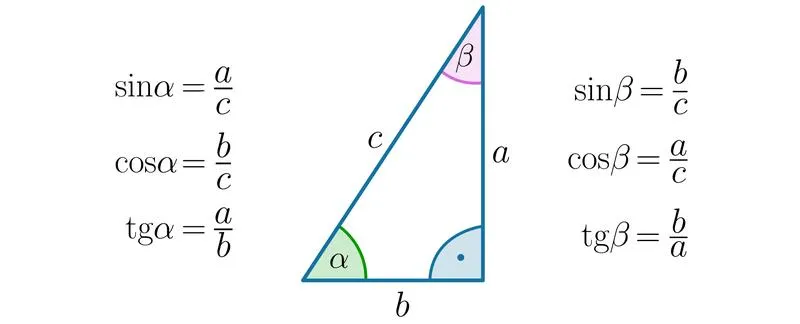
W królestwie trygonometrii, gdzie kąty oraz wartości liczbowe krążą wokół siebie jak tancerze na balu, warto zwrócić uwagę na jednego z najpopularniejszych uczestników tego wydarzenia – cosinus 60 stopni. Można go porównać do legendy wśród matematycznych postaci. Dlaczego tak jest? Powód jest prosty: jego wartość wynosi 0,5. Tak, dobrze widzisz! Nie trzeba być Einsteinem, by zauważyć, że to po prostu 1/2! Kto by pomyślał, że wzory matematyczne mogą być tak łatwe do zapamiętania, jak ulubiony przepis na naleśniki?
Spoglądając na tablice wartości funkcji trygonometrycznych, dostrzegasz, że cosinus dla kąta 60 stopni to jeden z wielu bohaterów, którzy zbierają laury blisko swojego kolegi, sinus 30 stopni. Ciekawe, prawda? Szkoła podstawowa zapewne nie nauczyła nas, że w rzeczywistości istnieje pewna magia w sposobie, w jaki funkcje trygonometryczne łączą się ze sobą. Nie chodzi tu jednak o magię znaną z książek o Harrym Potterze, lecz o porządek panujący w matematycznym wszechświecie!
Co takiego znaczy cosinus 60 stopni?
Cosinus 60 stopni to nie tylko liczba, ale także pojęcie, które otwiera drzwi do bardziej złożonych tematów w trygonometrii, takich jak układy współrzędnych oraz funkcje okresowe. Możesz wyobrazić sobie, że 0,5 działa jak klucz do zrozumienia, iż istnieją kąty, które nie są jedynie "w powietrzu", lecz mają swoje konkretne wartości w liczbach. Niektóre wartości, takie jak cosinus 30 stopni, czują się w tej grupie jak VIP-y, posiadające głębsze znaczenia, mimo że każdy kąt ma swoją niepowtarzalną osobowość!
W końcu, jeśli kiedykolwiek znajdziesz się zagubiony w oceanach kątów oraz funkcji, przypomnij sobie te proste wartości dla 30, 45 i 60 stopni. Te liczby będą jak Twoi matematyczni przyjaciele, którzy zawsze przybędą z pomocą, gdy życie matematyczne stanie się zbyt skomplikowane. A cosinus 60 stopni? To po prostu jeden z tych kumpli, którzy sprawiają, że uśmiech sam ciśnie się na twarz. Pamiętaj, że 60 stopni ma swoją wartość, a ta wartość to 0,5 – łatwe jak bułka z masłem, prawda?
Geometria w praktyce: Zastosowanie wartości cosinusa 60 stopni w trójkącie równobocznym
Geometria nie ogranicza się jedynie do skomplikowanych kątów oraz niezrozumiałych wzorów. W rzeczywistości stanowi praktyczne narzędzie, które otwiera drzwi do zrozumienia otaczającego nas świata. Weźmy na przykład trójkąt równoboczny, który doskonale ilustruje, jak wartości funkcji trygonometrycznych zyskują sens w naszym codziennym życiu. Dziś skoncentrujemy się na wartości cosinusa kąta, która sprawia, że wszystko wydaje się trójkątne! Mówimy oczywiście o jednym z najpopularniejszych kątów w matematyce, a więc chodzi o wartość cosinusa wynoszącą pół!
Trójkąt równoboczny wyróżnia się tym, że każdy jego kąt ma tę samą miarę. W tym kontekście zauważamy, jak przydatny okazuje się cosinus! Wiedząc, że w takim trójkącie kąt osiąga wartość odpowiadającą pięknej połowie, możemy swobodnie obliczać różne właściwości tego trójkąta. Na przykład, stosując wzór na cosinus, ustalamy długości boków oraz wysokość. Kto by pomyślał, że zabawa z trygonometrią może być taka prosta, prawda? Załóżmy więc, że mamy bok o długości "a". Wyrażając wysokość przez cosinus, zyskujemy lepsze zrozumienie, jak wysoko trójkąt może „wzbić się” w przestrzeń.
Praktyczne zastosowania cosinusa w trójkącie równobocznym

Gdy już opanujemy wartość cosinusa, otwierają się przed nami szerokie możliwości praktycznych zastosowań! Na przykład w budownictwie czy architekturze wykorzystanie trójkątów równobocznych oraz ich właściwości przyczynia się do tworzenia stabilnych budynków. Co więcej, znajomość właściwości kątów w takich trójkątach umożliwia lepsze projektowanie przestrzeni wewnętrznych, nietypowych mebli, a nawet elementów oświetlenia. Wygląda na to, że cosinus i trygonometria to nie tylko suche obliczenia, ale również prawdziwe narzędzia artysty!
- Stabilność budynków dzięki trójkątom równobocznym.
- Lepsze projektowanie przestrzeni wewnętrznych.
- Tworzenie nietypowych mebli oraz elementów oświetlenia.
- Wykorzystanie trygonometrii w sztuce i designie.
Na koniec, warto zwrócić uwagę na to, że choć matematyka nie zawsze cieszy się sympatią uczniów, jej praktyczne zastosowanie widoczne jest wszędzie. Zrozumienie cosinusa kąta, którego spotykamy na co dzień – od małych stołów po ogromne konstrukcje – ujawnia w niej pewną magię. Zatem, następnym razem, gdy zdecydujesz się na zbudowanie czegoś swojego, pamiętaj, że z pomocą trygonometrii wszystko staje się możliwe, a może nawet zabawne! Zainwestuj w swoją wiedzę, a może sam się zdziwisz, jak wiele właściwości geometrycznych kryje się w codziennych przedmiotach!
| Zastosowanie | Opis |
|---|---|
| Stabilność budynków | Wykorzystanie trójkątów równobocznych do tworzenia stabilnych konstrukcji. |
| Projektowanie przestrzeni | Lepsze projektowanie przestrzeni wewnętrznych. |
| Tworzenie mebli | Projektowanie nietypowych mebli oraz elementów oświetlenia. |
| Sztuka i design | Wykorzystanie trygonometrii w sztuce i designie. |
Matematyka w codziennym życiu: Gdzie spotykasz cosinus 60 stopni?
Matematyka obecna jest w naszym życiu w sposób zaskakujący. Wydaje się, że to jedynie zbiór reguł i wzorów umieszczonych na papierze, jednak paradoksalnie to właśnie w tych momentach, gdy jej nie oczekujesz, znajdziesz na przykład wspomniany cosinus kąta, którego prawdopodobnie unikasz podczas lekcji trygonometrii – mowa tu o sześćdziesięciu stopniach! Nie potrzebujesz być matematycznym geniuszem, aby dostrzec, że kąt ten pojawia się w licznych sytuacjach, od budowy domów, przez jazdę na nartach, aż po... przygotowywanie pysznych gofrów.
Wyobraź sobie, że stoisz przed gofrownicą i zastanawiasz się, ile ciasta wlać, aby gofry wyszły idealnie chrupiące. W takiej chwili z pomocą przychodzi trygonometria! Dzięki kątowi sześćdziesięciu stopni masz możliwość precyzyjnego obliczenia proporcji składników, ponieważ kto nie marzy o tym, by zjeść gofra w kształcie doskonałego trójkąta? Tak, zgadza się, ciasteczka mogą mieć formę kątów! Choć na początku to może brzmieć śmiesznie, matematyka potrafi nas zaskoczyć, szczególnie w kontekście kulinariów!
W jakich innych sytuacjach możemy spotkać kąt sześćdziesięciu stopni?
Kuchnia nie jest jedynym miejscem, gdzie matematyka ma swoje miejsce. Jeśli kiedykolwiek próbowałeś narysować trójkąt równoboczny, z pewnością zderzyłeś się z kątem sześćdziesięciu stopni. To określenie nie dotyczy jedynie teorii, ale także praktyki! Rozważmy budownictwo – pracując na wysokości, musisz zadbać o odpowiednie ustawienie kąta dachu, aby uniknąć zagrożenia. A skoro przy zabawach jesteśmy, to również jazda na nartach wymaga, abyś znał sposoby obliczania kąta nachylenia stoku – tutaj znowu pojawia się cosinus, aby zjazd z góry był elegancki jak gazela (albo przynajmniej stosunkowo bezpieczny). Nasz kąt towarzyszy nam niczym duch matematyki!

W ten sposób, na niefortunny sposób podążając przez życie, otaczamy się wszechobecną mocą goniących nas kątów. Cosinus sześćdziesięciu stopni staje się niczym superbohater, na którego zawsze możesz liczyć, niezależnie od tego, czy organizujesz przyjęcie, czy wznosisz dom. Kto wie, może gdy następnym razem spojrzysz na kawałek tortu, dostrzegasz w nim harmonijne powiązania z trygonometrią? Matematyka nieustannie czeka, by odkryć przed Tobą swoje tajemnice w codziennym życiu – tylko bądź przygotowany na niespodzianki!
Historia i rozwój trygonometrii: Jak odkrycie wartości cosinusa 60 stopni wpłynęło na naukę?
Trygonometria, mówiąc krótko, to nie tylko zawiłe wykresy i tajemnicze funkcje, ale również historia pełna odkryć, które na zawsze odmieniły oblicze matematyki. Jeśli spojrzymy na wartości funkcji trygonometrycznych dla najbardziej popularnych kątów, takich jak 30, 45 czy 60 stopni, to z łatwością dostrzegamy, jak te proste liczby mogą wpłynąć na całe pokolenia naukowców. Wśród nich szczególne miejsce zajmuje kąt sześćdziesięciu stopni, którego wartość cosinusa stanowi prawdziwy skarb matematyczny, otwierający drzwi do nowych odkryć.
Gdy naukowcy odkryli, że cosinus kąta sześćdziesięciu stopni równa się połowie, zaczęli dostrzegać niezwykłe powiązania między kątami a różnymi wielkościami geometrycznymi. Jak na to zareagowały umysły średniowiecznych uczonych? Można się domyślić, że z szokiem i podziwem! Wówczas rozpoczął się prawdziwy wysyp płaskich trójkątów, a trygonometria zyskała status lokomotywy rozwoju nauk ścisłych. Odkrycie, że sinus pięćdziesięciu stopni różni się od cosinusa sześćdziesięciu, zapoczątkowało nową erę w matematyce — wszystko nabrało nowego sensu!
Jak cosinus sześćdziesięciu stopni zrewolucjonizował trygonometrię
Funkcje sinus i cosinus dla kątów sześćdziesięciu i trzydziestu stopni zaczęły tworzyć fascynujący obraz trygonometrii. Odkrycia te nie tylko zainspirowały do dalszego zgłębiania tematu, ale także stanowiły podstawę dla rozwoju dziedzin takich jak astronomia czy inżynieria. Gdy naukowcy odkryli wartość cosinusa, wszystko zaczęło się kręcić — dosłownie! Krążące ciała niebieskie, fale dźwiękowe, a nawet najprostsze konstrukcje zostały opisane za pomocą tych wzorów. Można to porównać do dodania magicznego składnika do matematycznego przepisu!
Oczywiście nie ma cienia wątpliwości, że odkrycie wartości cosinusa kąta sześćdziesięciu stopni miało ogromny wpływ na rozwój nauki. Choć to tylko zwykły kąt, otworzył przed nami nieskończoność możliwości! Dzięki temu trygonometria stała się integralną częścią wielu dziedzin. Korzystając z jej wartości, potrafimy obliczać odległości, przewidywać ruchy planet, a także rozwiązywać problemy niegdyś uważane za niemożliwe do rozwiązania. Tak, to właśnie dzięki jednemu z najprostszych kątów matematyka zyskała nowe życie! A dziś? W tej dziedzinie gromadzi się więcej wiedzy niż w niejednej izbie przyjęć!
Poniżej przedstawiamy przykłady zastosowań wartości cosinusa i sinus w różnych dziedzinach nauki:
- Obliczanie odległości między ciałami niebieskimi w astronomii
- Analiza fal dźwiękowych w akustyce
- Projektowanie struktur inżynieryjnych w budownictwie
- Modelowanie ruchu planet w astrodynamice