Drgania to temat, który brzmi nie tylko w murach uczelni, lecz również w naszym codziennym życiu. Nawet nie zdając sobie z tego sprawy, drgania towarzyszą nam od rana do wieczora! Gdy kołysze się tramwaj, gdy rytmicznie stuka klawiatura w biurze, czy wtedy, gdy głośnik gra na imprezie – wszystko oscyluje w pewien sposób. Najważniejsze jest, abyś zrozumiał pojęcia krążące wokół drgań: okres, częstotliwość i ich wzajemne powiązania. Tak jak w przypadku kawy, im lepiej rozumiesz podstawowe składniki, tym większa energia płynie z tego doświadczenia!
- Drgania są obecne w naszym codziennym życiu i można je zrozumieć poprzez pojęcia okresu i częstotliwości.
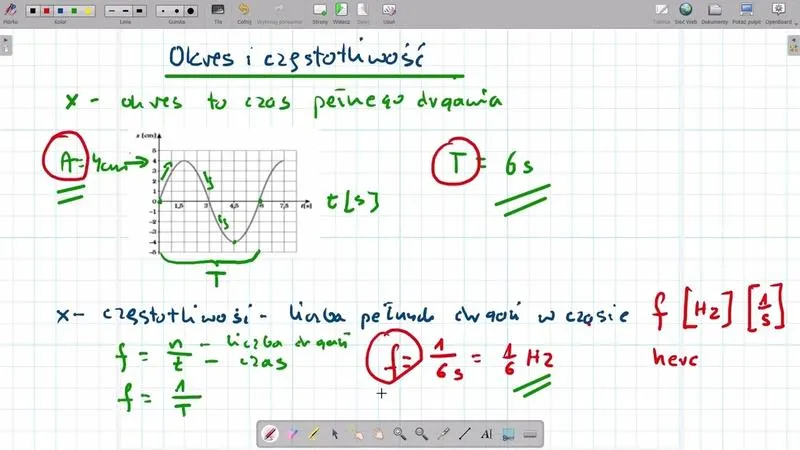
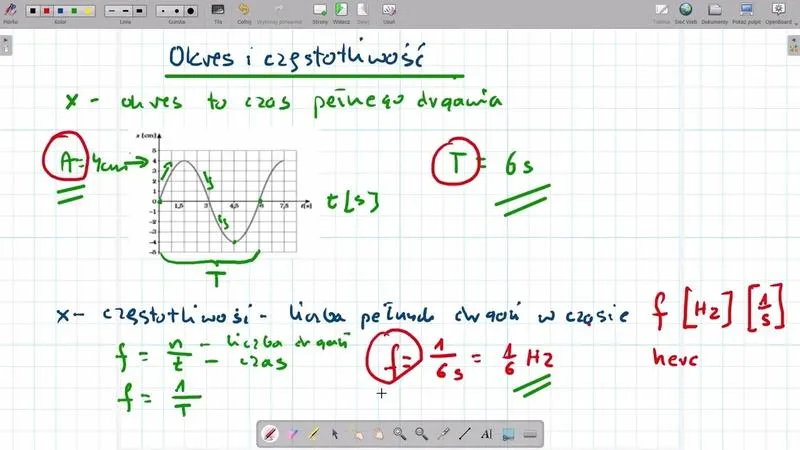
- Okres drgań (T) to czas potrzebny do wykonania jednego pełnego cyklu, podczas gdy częstotliwość (f) to liczba cykli w jednostce czasu.
- Aby obliczyć częstotliwość, można użyć wzoru f = 1/T, podczas gdy T można obliczyć na podstawie częstotliwości.
- Wzory na obliczanie okresu drgań obejmują: T = 2π√(l/g) dla wahadła matematycznego oraz T = 2π√(m/k) dla wahadła sprężynowego.
- Praktyczne zastosowanie drgań obejmuje zarówno huśtawki, jak i instrumenty muzyczne, gdzie liczba drgań wpływa na odczuwane dźwięki.
- Częste błędy w obliczeniach okresu drgań wynikają z niewłaściwego pomiaru i braku stabilności wahadła.
- Kluczowe zasady obliczeń obejmują: stabilność wahadła, wystarczającą liczbę cykli pomiarowych oraz właściwe ustawienie wahadła.
Okres drgań, oznaczany literą T, to czas, który potrzebuje układ drgający, aby przejść przez jeden pełny cykl i wrócić do punktu, w którym zaczął. Możesz to zobrazować na przykładzie wahadła zegara: od wychylenia w prawo przede wszystkim do wychylenia w lewo, a następnie z powrotem – wyobraź sobie takie piruety na huśtawce! Częstotliwość natomiast określa liczbę drgań, które układ wykonuje w ciągu sekundy i mierzy się ją w hercach (Hz). Zauważ, że im krótszy czas trwania okresu, tym więcej drgań następuje w jednostce czasu. Można to rozumieć jako przepis na idealną symfonię: odpowiednia częstotliwość do perfekcyjnego rytmu!
Jak obliczyć okres i częstotliwość drgań?
Obliczanie okresu i częstotliwości drgań to nic innego jak ciekawa zabawa w matematykę z dodatkiem fizyki! Aby obliczyć częstotliwość, wystarczy zastosować prosty wzór f = 1/T, gdzie T to okres. Jeśli nasz zegarowy wahadłowiec ma T=2s, to częstotliwość f wyniesie 0,5 Hz, czyli jedno drganie występuje co dwie sekundy. W praktyce możesz obliczyć te parametry również poprzez podzielenie liczby drgań przez czas ich trwania, co pozwala uzyskać znacznie szerszy obraz ambicji wahadła.
Zrozumienie tych podstawowych pojęć nie tylko poszerza naszą wiedzę o drganiach, ale także umożliwia zastosowanie ich w różnych dziedzinach – od budownictwa po inżynierię! Choć może wydawać się to zawiłe, pamiętaj, że drgania działają jak zespół muzyczny: zgrany harmonogram i odpowiednia częstotliwość mogą stworzyć piękną melodię, i to nie tylko w twoim radio! Dlatego wzbogać swoją wiedzę, a wszystko stanie się jasne i przejrzyste.
Wzory na obliczanie okresu drgań – krok po kroku
Obliczanie okresu drgań to temat, który potrafi sprawić, że nawet najbardziej zagubiony student poczuje się jak Albert Einstein. Nie oszukujmy się – na pierwszy rzut oka może to wydawać się nieco skomplikowane, ale z odpowiednim podejściem zrozumienie tego zagadnienia staje się równie proste jak zrobienie kawy bez filiżanki. Zacznijmy od wyjaśnienia kilku podstawowych pojęć, takich jak częstotliwość i okres. Dla tych, którzy jeszcze nie wiedzą, okres (oznaczany literą T) to czas potrzebny na wykonanie jednego pełnego cyklu drgań. Częstotliwość z kolei stanowi odwrotność okresu i oznacza, ile razy drganie powtarza się w ciągu sekundy. Prawda, że to proste jak dwa plus dwa?
Przechodzimy teraz do szczegółów, czyli jak oblicza się T? Oczywiście istnieje kilka formuł, ale skupmy się na najprostszej. Dysponując częstotliwością, wystarczy zastosować wzór T = 1/f, gdzie f to częstotliwość wyrażona w hercach. Natomiast jeśli wolisz bardziej analityczne podejście, możesz policzyć liczbę drgań w określonym czasie i podzielić ją przez ten czas. To naprawdę prosto, prawda? To jak obliczanie wieku - wystarczy policzyć, ile masz lat, i voilà! Oczywiście tylko dla tych, którzy pamiętają, kiedy się urodzili.
Wzory i ich zastosowanie w praktyce
Teraz, gdy już rozumiemy, jak obliczyć okres drgań, czas na praktykę. W ruchu wahadła matematycznego wykorzystujemy wzór T = 2π√(l/g), gdzie l to długość wahadła, a g to przyspieszenie ziemskie. W skrócie, im dłuższe wahadło, tym dłużej się huśta! W przypadku wahadła sprężynowego wzór przedstawia się jako T = 2π√(m/k), gdzie m to masa ciężarka, a k to współczynnik sprężystości. Możesz nawet wyobrazić sobie, jak sprężynka „prosi” ciężarek, aby się nie bujał zbyt mocno, ponieważ w przeciwnym razie czas trwania zabawy znacznie się wydłuży!
Pamiętaj, że w zależności od typu wahadła, z jakim masz do czynienia, wzory mogą się różnić, a każdy z nich dostarcza nowych informacji na temat drgań i ruchu. Utrwalenie tej wiedzy oraz umiejętność jej zastosowania w praktyce to klucz do sukcesu w każdym fizycznym wyzwaniu, które napotkasz w trakcie edukacyjnej podróży. Na koniec pamiętaj, że bez względu na wybrany wzór, im więcej pomiarów wykonasz, tym mniejsze będą Twoje błędy pomiarowe. Bujać się to przecież bardzo matematyczne, a może nawet lekko filozoficzne, prawda?
Poniżej przedstawiam kilka kluczowych wzorów dotyczących obliczania okresu drgań:
- Wzór dla wahadła matematycznego: T = 2π√(l/g)
- Wzór dla wahadła sprężynowego: T = 2π√(m/k)
- Wzór na obliczenie okresu z częstotliwości: T = 1/f
Praktyczne przykłady zastosowania – od huśtawek po instrumenty muzyczne
Drgania otaczają nas z każdej strony – zaczynając od huśtawek w parku, które zachęcają do beztroskiego bujania, aż po instrumenty muzyczne składające się z wielu drgających elementów. Być może nigdy nie zastanawialiście się, dlaczego huśtawka buja się w określony sposób lub jak to się dzieje, że dźwięk gitary uzależnia? Wszystko sprowadza się do liczby drgań i ich częstotliwości! W świecie fizyki drgania kryją w sobie magię, ponieważ umożliwiają nam cieszenie się relaksującym bujaniem lub piękną muzyką.
Drgania w huśtawek i ich magia
Wyobraźmy sobie: znajdujemy się na placu zabaw, w tle rozbrzmiewają radosne okrzyki dzieci, a my wsiadamy na huśtawkę. Z każdym wychyleniem huśtawka przekształca energię potencjalną w kinetyczną. Przyczyną tego niezwykłego zjawiska są drgania periodyczne, które nieustannie nam towarzyszą. Im wyżej się unosimy, tym szybciej wracamy do bazy. Okres drgań określa czas potrzebny na powrót do punktu wyjścia. Prostą zasadą jest to, że długość huśtawki wpływa na czas bujania – ogromna radość z tak małej reguły!
Muzyczne drgania na scenie
A co z instrumentami muzycznymi? Gdy uderzamy strunę gitary, wibruje ona, a te drgania przekształcają się w fale dźwiękowe docierające do naszych uszu. Im szybciej drgają, tym wyższa częstotliwość dźwięku – możecie to sami zauważyć podczas gry na różnych strunach. Niska struna produkuje cięższe dźwięki, natomiast wysoka struna daje lekkie, radosne tonacje. Dlatego właśnie podczas jam session tak ważna jest różnorodność! Muzyczne drgania odgrywają niezwykle istotną rolę, a dzięki nim cały świat dźwięków staje się na wyciągnięcie ręki.
Podsumowując, drgania to nie tylko huśtawki w parku, ale także melodia w naszych sercach. Od beztroskiego bujania na świeżym powietrzu po występy na scenie, drgania towarzyszą mi na każdym kroku. Dlaczego więc nie połączyć tych dwóch światów? Wyobraźcie sobie urokliwą huśtawkę, na której bujamy w rytm muzyki! A może zorganizujemy mini koncert na placu zabaw? Wystarczy odrobina wyobraźni, a drzwi do radosnych drgań otworzą się na oścież!
| Element | Opis | Wzór na okres drgań |
|---|---|---|
| Huśtawka | Drgania periodyczne, przechodzenie energii potencjalnej w kinetyczną. | T = 2π√(L/g) |
| Instrumenty muzyczne | Drgania strun przekształcające się w fale dźwiękowe. | T = 1/f |
Częste błędy w obliczeniach okresu drgań – jak ich unikać?
Obliczanie okresu drgań stanowi temat, który może wydawać się prosty, ale niejednokrotnie zaskakuje miłośników zawirowaniami na matematycznej ścieżce. Wśród najczęściej popełnianych błędów zauważamy pomijanie istotnych wartości przy pomiarach. Wyobraźmy sobie sytuację, w której z niecierpliwością wkładamy wahadło do doświadczenia, jednak zapominamy o odpowiednim ustawieniu stoperów. Czasami, zamiast korzystać z kilku cykli, stresujemy się, licząc jedynie pierwsze drganie. W rezultacie końcowym możemy uzyskać bardziej komiczne efekty niż naukowe! Warto podkreślić, że mistrzostwo w pomiarze ma znaczenie, a nie brawura.
Innym częstym faux pas, które pojawia się w obliczeniach, jest niewłaściwe usytuowanie wahadła. Bez wątpienia wahadło zasługuje na odpowiednie warunki, niczym artysta. Kiedy zatem wsadzimy je w kąt, gdzie będzie musiało zmagać się z zewnętrznymi siłami, jak grawitacja czy wiatr, wszystkie skomplikowane wzory mogą okazać się bezużyteczne. Dlatego warto dbać o stabilne powierzchnie oraz unikać nagłych ruchów, które mogą zakłócić pomiar. Kto by pomyślał, że fizyka tak bardzo zależy od drobiazgów?
Kluczowe zasady przy obliczeniach okresu drgań
Aby osiągnąć sukces w obliczeniach okresu drgań, niezbędne staje się zrozumienie zależności między długością wahadła a jego okresem. Niestety, wiele osób zapomina, że dłuższe wahadło zawsze wiąże się z dłuższym okresem — jakby każda z długości starała się zdobyć wyżyny w sportowej rywalizacji. Gdy zrozumiemy ten związek, obliczenia nabiorą większej klarowności, a przyszłe pomiary będą znacznie bardziej precyzyjne. Zamiast dryfować w nieprzejrzystym oceanie danych, lepiej krok po kroku mierzyć zjawiska i zyskać pewność w obliczeniach.
Oto niektóre z kluczowych zasad, które warto uwzględnić podczas obliczeń okresu drgań:
- Dbanie o stabilność wahadła i jego otoczenia.
- Zastosowanie wystarczającej ilości cykli pomiarowych.
- Zapewnienie, że wahadło jest prawidłowo ustawione i nie podlega zakłóceniom.
- Dokładne uwzględnienie długości wahadła w obliczeniach.
Podsumowując, pomiary okresu drgań stanowią sztukę, która wymaga zarówno matematycznej precyzji, jak i cierpliwości oraz zrozumienia fizyki. Unikanie typowych błędów, takich jak pomijanie kilku cykli czy nieodpowiednie dopasowanie jednostek, pozwoli nam oszczędzić nerwy i frustrację. Z apetytem na wiedzę oraz skrupulatnością w pomiarach możemy oswoić drgania na własnych zasadach. Wówczas każdy nowy pomiar stanie się dla nas bezbłędnym dziełem sztuki!
Wkrótce każdy z nas zyska miano mistrza drgań — prawdziwego fachowca w tym zakresie!
Pytania i odpowiedzi
Co to jest okres drgań i jak można go zobrazować?
Okres drgań, oznaczany literą T, to czas potrzebny układowi drgającemu, aby przejść przez jeden pełny cykl. Można to zobrazować na przykładzie wahadła zegara, które wychyla się w prawo, następnie w lewo, a potem wraca do punktu wyjścia.
Jak oblicza się częstotliwość w kontekście drgań?
Aby obliczyć częstotliwość, należy zastosować wzór f = 1/T, gdzie T to okres drgań. W praktyce można też podzielić liczbę drgań przez czas ich trwania, co dostarcza szerszego obrazu ruchu układu drgającego.
Jakie są wzory na obliczanie okresu drgań dla różnych układów?
Dla wahadła matematycznego wzór to T = 2π√(l/g), a dla wahadła sprężynowego T = 2π√(m/k). Dodatkowo można używać wzoru T = 1/f, gdy mamy dane dotyczące częstotliwości drgań.
Co wpływa na długość okresu drgań w przypadku huśtawek?
Długość huśtawki ma bezpośredni wpływ na czas bujania - im dłuższa huśtawka, tym dłużej trwa jej okres drgań. Wraz z większą długością wahadła, układ drgający potrzebuje więcej czasu, aby wrócić do punktu wyjścia.
Jakie są najczęstsze błędy popełniane podczas obliczania okresu drgań?
Do najczęstszych błędów należy pomijanie istotnych wartości przy pomiarach oraz niewłaściwe ustawienie wahadła. Utrzymanie stabilności wahadła oraz wykonywanie pomiarów przez kilka cykli pozwala uniknąć niepoprawnych wyników.