W świecie matematyki liczby odznaczają się swoimi unikalnymi osobowościami. Niektóre z nich jawią się jako skromne, inne przyciągają uwagę krzykliwością, a jeszcze inne emanują tajemniczością. Każda cyfrowa postać odgrywa ważną rolę w naszych obliczeniach oraz definicjach; przy czym jedne są bardziej złożone, a inne mniej. Na przykład, liczba 0 działa jak matematyczny ninja, wprowadzając najdziwniejsze triki, z kolei liczba 1 przemienia się w superbohatera, umożliwiając nam wzniesienie się do potęgi. Chociaż liczby nie potrafią mówić, ich symbole docierają tam, gdzie słowa nie mają wstępu.
W matematyce liczby reprezentują różnorodne pojęcia, które łączą się z nimi niczym przyjaciele w dobrze znanym klubie. Na przykład, liczby całkowite stanowią jakby rodzinę, zawsze zwaśnioną między sobą w obozach dodatnich i ujemnych. Z kolei liczby niewymierne przybierają tajemnicze formy, które nieustannie zaskakują nas swoimi nieskończonymi rozwinięciami dziesiętnymi. A logarytmy? One przypominają czary! Mamy logarytm dziesiętny, naturalny oraz wiele innych, które pomagają nam odnaleźć się w zawirowaniach wzorów. Matematyka w sercu, a liczby na końcu języka!
Symbolika liczb w matematyce: co oznaczają?
Każde matematyczne pojęcie można przedstawić za pomocą liczbowych symboli. Na przykład całka (∫) zdaje się wołać: „Hej, oblicz mi pole pod tym wykresem!”. Po opanowaniu umiejętności rozpoznawania tych matematycznych znaków, otwierasz drzwi do fascynującego świata, w którym liczby prowadzą nas do rozwiązań równań oraz podatków, a to wszystko bez większego stresu. Używając symboli takich jak ∑, Δ czy ≡, wzbogacasz swoje zrozumienie rzeczywistości, wplatając je w swoją codzienność.
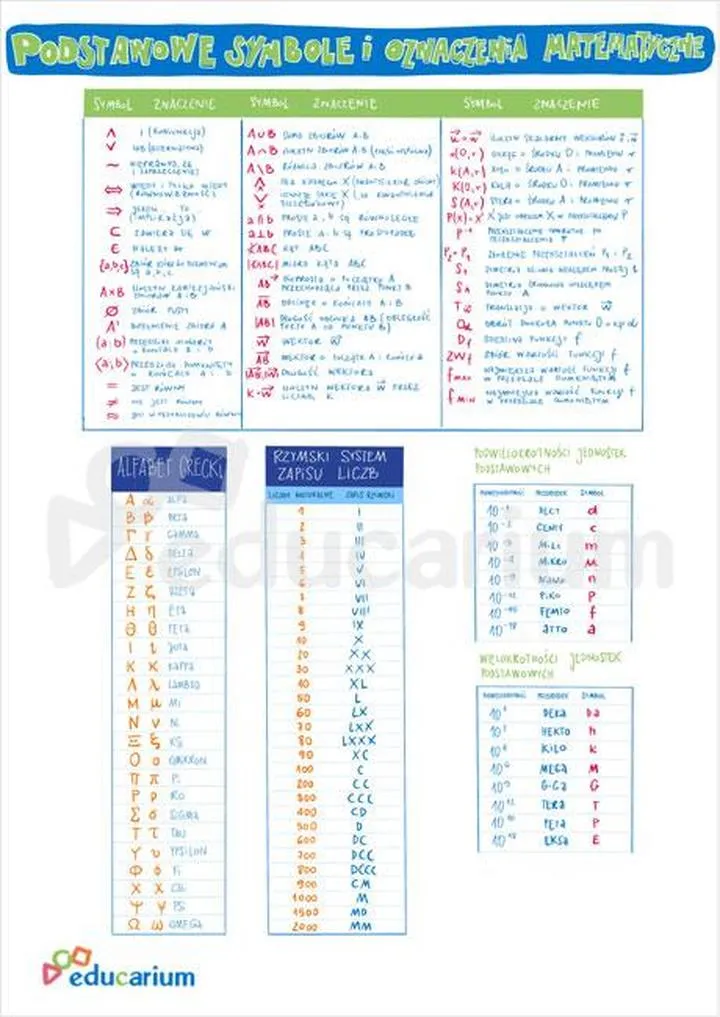
Nie możemy jednak zapomnieć o nierównościach (>, <, ≤, ≥), które przypominają matematyczne plotki - zawsze otaczają nas w każdej sytuacji. Dzięki nim zyskujemy wiedzę o tym, co jest większe, a co mniejsze, co pozwala nam porównywać rzeczy, niczym przyjaciół w podstawówce. Gdyby liczby tworzyły swoje towarzystwo, na pewno panowałby w nim śmiech, a to, że potrafią komunikować się przez symbole, czyni je jeszcze bardziej zdumiewającymi. Dlatego właśnie zrozumienie symboliki liczb stanowi klucz do odkrywania niekończących się możliwości, które oferuje matematyczny świat!
Operatory matematyczne: Kluczowe znaki i ich funkcje
Operatory matematyczne odgrywają rolę alfabetu emocjonalnego matematyki, ponieważ każdy z nich ma swoje unikalne zadanie i znaczenie. Na początek przyjrzyjmy się najpopularniejszym operatorom, czyli plusowi (+) oraz minusowi (-). Plus staje się przyjacielem, który dodaje nam energii, a kiedy widzimy go w równaniu, czujemy, że coś zyskujemy. Minus natomiast często sprawia nam kłopoty, jednak bez niego życie stałoby się zbyt proste. Dlatego przy dodawaniu jabłek lub odejmowaniu kłopotów, te operatory pozostają niezastąpione!
Nie zapominajmy również o mnożeniu (·) oraz dzieleniu (÷), które wprowadzają naprawdę ekscytujące elementy do matematycznych przygód. Mnożenie przypomina zapraszanie na imprezę – gromadzi wszystkich i tworzy z tego wielką frajdę. Natomiast dzielenie można porównać do rozdzielania kawałków tortu – zawsze lepiej, gdy wszyscy dostają swoją równą część! Bez względu na to, czy przebywamy w szkole, biurze, czy po prostu rozmyślamy o życiu, używanie tych operatorów znacząco upraszcza nasze logiczne myślenie.
Symbole dalszych operatorów: znaczenie i zastosowanie
Warto także wspomnieć o mniej znanych, lecz równie istotnych operatorach. Mamy na przykład całkę (∫), która pełni funkcję matematycznego narzędzia, usuwając granice i umożliwiając nam zanurzenie się w tajemnice pól pod krzywymi. Nie możemy pominąć symboli nierówności (≤, ≥), które znacząco wspierają nas w porównaniach matematycznych. Kiedy widzimy ≥, odczuwamy satysfakcję, jakbyśmy spełniali nasze marzenia – wszystko, co robimy, przynosi nam bonusy! Te znaki funkcjonują jak strażnicy porządku, pomagając określić, „jak bardzo” coś się zmienia.
- Całka (∫) - narzędzie do analizy pól pod krzywymi
- Nierówności (≤, ≥) - służą do porównań matematycznych i określania warunków
- Logarytmy - tajne hasła do zrozumienia potęg i obliczeń
- Symbole równości (=) - wskazują na zgodność wartości
Na zakończenie warto zwrócić uwagę na specjalne operatory, takie jak logarytmy i symbole równości. Logarytmy działają jak tajne hasła do zrozumienia potęg oraz obliczeń, co znacznie ułatwia rozwiązywanie złożonych problemów bez zbędnego stresu. Z drugiej strony, znaki równości przypominają nam, że czasami wszystko, co mamy, naprawdę się zgadza. Jak zatem widzisz, operatory matematyczne to nie tylko znaki – to skomplikowana sieć relacji, która sprawia, że świat matematyki staje się tak fascynujący. Bez nich nasza praca z liczbami przypominałaby malowanie w odcieniach szarości – nudno i monotonnie!
Zrozumienie zmiennych: Rola liter w matematycznych równaniach
Zmienne w matematyce przypominają bohaterów w doskonale napisanym filmie, ponieważ każda z nich odgrywa swoją unikalną rolę. Choć na pierwszy rzut oka mogą wydawać się jedynie literkami, ich obecność ma ogromne znaczenie dla zrozumienia matematycznych koncepcji. Wyobraź sobie matematykę jako skomplikowany przepis kulinarny, w którym zmienne pełnią rolę składników. Na przykład zmienna „x” działa jak tajemniczy składnik, którego ilość musisz odkryć, aby danie, czyli równanie, wyszło doskonale. Dzięki takim literkom mamy możliwość tworzenia równań, które pomagają rozwiązywać różnorodne problemy, od obliczania odległości po planowanie budżetu na wakacje. Zatem zadawanie równań staje się równie emocjonujące jak rozwiązywanie zagadek kryminalnych!
Przechodząc do innych aspektów, niektóre zmienne wyróżniają się wszechstronnością, ponieważ mogą reprezentować różne wartości w różnych kontekstach, niczym aktorzy odgrywający różne role. Na przykład w jednym równaniu „m” pełni rolę współczynnika prostoliniowego, podczas gdy w innym staje się wskaźnikiem wzrostu w badaniach. Dzięki elastycznemu podejściu do zmiennych matematyka staje się bardziej kreatywna i praktyczna. To podejście pozwala zrozumieć, jak jeden symbol może mieć tak wiele zastosowań! Czasami warto traktować te literki jako naszych sprytnych pomocników, którzy pomagają nam poruszać się przez zawirowania liczb podczas nauki.
Rola zmiennych w równaniach matematycznych
Warto zauważyć, że zmienne mogą przyjmować różne role; czasami funkcjonują niczym superbohaterowie, ponieważ pomagają nam rozwiązywać złożone problemy matematyczne. Weźmy na przykład całki i nierówności – to potężne narzędzia w rękach matematyka. Symbole takie jak ∫ i ≥ odpowiadają na fundamentalne pytanie: „jaka jest wartość x?”. Tak więc zmienne pozwalają stworzyć złożony obraz matematycznych relacji, które nie są jedynie zbiorami liczb, ale dynamicznymi strukturami opartymi na zależnościach i powiązaniach.
Należy również pamiętać, że każde „x” i „y” symbolizuje nadzieje i marzenia młodych matematyków, którzy podejmują wyzwania związane z rozwiązywaniem skomplikowanych zagadek, niczym w rzeczywistym życiu. Co więcej, zrozumienie ich znaczenia sprawia, że matematyka przestaje być czarną magią, a staje się fascynującą przygodą. Dzięki literom zmiennej oraz ich właściwej interpretacji, każdy może usiąść w fotelu głównego bohatera matematycznego filmu i odkrywać tajemnice, które kryje ta wspaniała dziedzina nauki!
Matematyka a logika: Oznaczenia w wyrażeniach logicznych i ich znaczenie
Matematyka, uważana za królową nauk, zyskuje miano tego, co najważniejsze, a logika stanowi jej niezawodną przyjaciółkę. Choć brzmi to jak tytuł klasycznego kanału YouTube o podróżach, to właśnie te dwie dziedziny idealnie się uzupełniają. W efekcie tworzą zjawiska, które potrafią być więcej niż tylko literką z alfabetu greckiego. Bez tych kluczy z pewnością byłoby trudno, niczym w restauracji zamawiając burgera, nie znając menu – nie wiadomo, co się dostanie! Na przykład, kiedy natrafisz na symbol Δ, wiedz, że mamy na myśli coś więcej niż tylko literkę z alfabetu greckiego. Ten symbol oznacza różnicę, a w kontekście życia – zmiany, jak na przykład zmiany pogody, co może zmusić nas do wyjścia z parasolem.

Przechodząc do logiki, wirujemy w grze, która może przypominać szkołę baletową! Oznaczenia takie jak >, <, ≥ czy ≤ to bowiem magicze różdżki, które umożliwiają nam opis relacji pomiędzy cyframi. Dzięki tym znakom zyskujemy klarowną hierarchię, co pozwala na dokładne porównania. Kiedy na przykład twierdzimy, że "x ≥ 5", otwieramy sobie drogę do obliczeń, mając pewność, że x musi być większe lub równe pięciu. To sprawdza się nie tylko w praktyce matematycznej, lecz także w codziennym życiu – pamiętaj, że wokół mnie nie ma pięciu osób znających kryptowaluty, lecz każdy z nas dysponuje swoją cyfrą i swoimi wartościami!
Oznaczenia logiczne i ich magia w codziennym życiu
W logice matematycznej symbole to nie tylko interesujące znaki, ale także skuteczne narzędzia, które prowadzą nas do błyskotliwych wniosków. Oznaczają one różnorodne relacje i powiązania między elementami. Symbole takie jak ∧ (i) oraz ∨ (lub) to obszary, w których krzyżują się marzenia i ambicje – zasadniczo mówią „jeśli to, to tamto”. Jak zatem możemy przekształcić te abstrakcyjne symbole w coś przydatnego? Na przykład, mówiąc „jeśli dzisiaj pada deszcz ∧ jutro będzie słońce, to wybieram dzień na relaks”, możemy wprowadzić logikę do codziennych wyborów. Jeśli potrafimy połączyć logiczne wyrażenia z życiową rzeczywistością, otwieramy drzwi do lepszego zrozumienia świata po drugiej stronie matematyki!
Oto kilka przykładów zastosowań oznaczeń logicznych w codziennym życiu:
- Jeśli pada deszcz, to używam parasola.
- Jeżeli mam czas, to wykonam zadanie domowe.
- Gdy jest słonecznie, to idziemy na spacer.

Podsumowując, znajomość oznaczeń matematycznych i logicznych obdarza nas supermocami. Już nie traktujemy równań i symboli wrogo – zaczynamy je rozumieć, a nawet, co zaskakujące, doceniać! W końcu, kim bylibyśmy bez naszej ulubionej całki czy prostej nierówności? Można by pomyśleć, że to tylko plasterek na bardzo poważne rany matematyczne, lecz każdy znak ma swoją historię – to właśnie czyni matematykę tak fascynującą! Dlatego bądźmy otwarci na te logiczne oznaczenia, traktując je jak bohaterów w naszej własnej matematycznej opowieści.
| Symbol | Znaczenie | Przykład zastosowania |
|---|---|---|
| Δ | Różnica, zmiana | Zmiany pogody, które mogą wymagać zabrania parasola. |
| > | Większe niż | Jeżeli x > 5, to x jest większe od pięciu. |
| < | Mniejsze niż | Jeżeli y < 10, to y jest mniejsze od dziesięciu. |
| ≥ | Większe lub równe | Jeżeli x ≥ 5, to x musi być większe lub równe pięciu. |
| ≤ | Mniejsze lub równe | Jeżeli y ≤ 15, to y musi być mniejsze lub równe piętnastu. |
| ∧ | I (konjunkcja) | „Jeśli dzisiaj pada deszcz ∧ jutro będzie słońce, to wybieram dzień na relaks.” |
| ∨ | Lub (alternatywa) | „Jeżeli mam czas ∨ chcę odpocząć, to wykonam zadanie domowe.” |
Źródła:
- https://bibliotekawolontariatu.pl/symbole-matematyczne-bez-tajemnic-%CE%B4-%E2%88%AB-%E2%89%A5-co-znacza/
Pytania i odpowiedzi
Jakie znaczenie mają liczby w matematyce według artykułu?
Liczby w matematyce odznaczają się swoimi unikalnymi osobowościami i odgrywają ważną rolę w obliczeniach oraz definicjach. Różne liczby reprezentują różnorodne pojęcia, jak na przykład liczby całkowite, które tworzą rodzinę pełną sporów między dodatnimi a ujemnymi wartościami.
Co oznacza symbol całki (∫) w kontekście matematycznym?
Symbol całki (∫) jest matematycznym narzędziem, które umożliwia obliczenie pola pod wykresem funkcji. Dzięki niemu można poznawać tajemnice pól i analiza całek staje się kluczowym elementem w matematyce.
Jaką rolę pełnią zmienne w matematyce?
Zmienne w matematyce działają jak bohaterowie w filmie, ponieważ odgrywają unikalne role, ułatwiając zrozumienie różnych koncepcji. To właśnie dzięki zmiennym możemy tworzyć równania, które pomagają rozwiązywać różnorodne problemy, takie jak obliczanie odległości czy planowanie budżetu.
Jakie operatory matematyczne są szczególnie ważne i jakie mają znaczenie?
Do kluczowych operatorów matematycznych należy plus (+) i minus (-), które reprezentują dodawanie i odejmowanie. Mimo że minus może sprawiać kłopoty, to bez obu operatorów życie matematyczne byłoby zbyt proste.
Jakie są przykłady zastosowania oznaczeń logicznych w codziennym życiu?
Oznaczenia logiczne, takie jak „∧” oznaczające "i" oraz „∨”, które oznacza "lub", tworzą relacje pomiędzy elementami w codziennych decyzjach. Na przykład, zdanie „jeżeli pada deszcz ∧ jutro będzie słońce, to wybieram dzień na relaks” ilustruje zastosowanie logiki w praktyce.