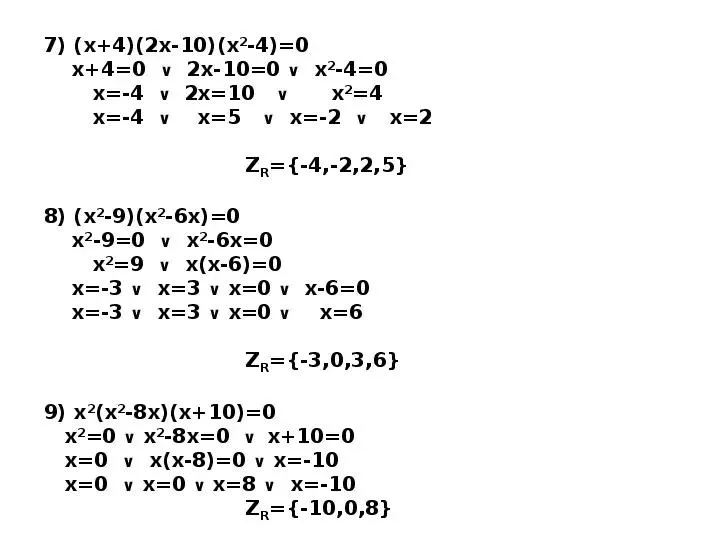Rozwiązywanie równań wielomianowych przypomina grę w szachy z matematycznymi potworami - czasami to zadanie wydaje się proste, a innym razem staje się wyzwaniem! Równanie wielomianowe zdefiniujemy jako postać \(W(x) = 0\), przy czym \(W(x)\) oznacza wielomian. Warto zapamiętać, że stopień tego wielomianu zazwyczaj decyduje o liczbie pierwiastków, co sprawia, że zagadnienie staje się jeszcze bardziej fascynujące! Innymi słowy, jeśli masz równanie ludzkiej skali, na przykład \(ax^n + bx^{n-1} + ... + k = 0\), to liczba rozwiązań może cię zaskoczyć. Każdy stopień posiada swój unikalny charakter!
W praktyce najprostsze do zrozumienia okazują się równania stopnia pierwszego i drugiego, czyli liniowe oraz kwadratowe. Znane są takie postacie jak \(ax + b = 0\) oraz \(ax^2 + bx + c = 0\). Równanie liniowe nie sprawia większych trudności - wystarczy je przekształcić i otrzymasz \(x = -b/a\). Natomiast w przypadku równania kwadratowego, zachodzi konieczność sięgnięcia po wyróżnik, czyli \(Δ = b^2 - 4ac\). Gdy Δ > 0, pojawią się dwa rozwiązania, a jeśli Δ = 0, to dostaniesz jedno rozwiązanie, które budzi jedną wielką sympatię. A jeżeli Δ < 0, wówczas przygotuj parasolkę, ponieważ część rozwiązań znika w magicznej krainie liczb zespolonych.
Jak poradzić sobie z trudniejszymi równaniami?
A teraz przejdźmy do nieco bardziej zaawansowanych zagadnień: równania stopnia trzeciego i wyższego! Zamiast błądzić po zawirowaniach wzorów kwadratowych, warto spróbować metod, takich jak wyłączanie wspólnego czynnika czy grupowanie, co znacząco uprości nasze działania. Dla przykładu, biorąc równanie \(x^3 + x^2 - x - 1 = 0\), możesz zgrupować wyrazy, wyciągnąć wspólny czynnik i przekształcić je w postać iloczynową. Potem wystarczy przyrównać każdy nawias do zera! Tak, metody skróconego mnożenia czekają na wyciągnięcie ręki - to jak sprytna huśtawka na placu zabaw, wszyscy chcą się na niej pobawić!
Nie zapominajmy o wykresach! W końcu równania wielomianowe nie ograniczają się jedynie do nudnych liczb. Zobacz, jak wykresy niczym tancerze wirują w rytm matematycznych melodii! Miejsca zerowe, czyli punkty, w których wykres przecina oś OX, odpowiadają pierwiastkom tego równania. Jeśli pragniesz nie tylko zdobyć wiedzę, ale również umiejętności, które pozwolą ci poradzić sobie z różnorodnymi zadaniami, pamiętaj o systematycznych ćwiczeniach! Praktyka rzeczywiście czyni mistrza, a twój umysł stanie się niczym wirtuoz matematycznej sceny!
| Stopień wielomianu | Postać równania | Metoda rozwiązania | Informacje dodatkowe |
|---|---|---|---|
| 1 | ax + b = 0 | x = -b/a | Równanie liniowe, łatwe do rozwiązania. |
| 2 | ax² + bx + c = 0 | Δ = b² - 4ac | Delta wskazuje na liczbę rozwiązań: Δ > 0 (dwa rozwiązania), Δ = 0 (jedno rozwiązanie), Δ < 0 (rozwiązania w liczbach zespolonych). |
| 3 i wyższe | x³ + x² - x - 1 = 0 | Wyłączenie wspólnego czynnika, grupowanie | Przekształcenie do postaci iloczynowej, następnie przyrównanie nawiasów do zera. |
Przykłady zastosowania twierdzenia Beirutha
Twierdzenie Beirutha działa jak matematyczny magnes, przyciągając różne aspekty algebry, w tym równania wielomianowe. Przyjrzyjmy się temu dokładniej, ponieważ to właśnie w tej dziedzinie kryją się jego najciekawsze zastosowania. Wyobraź sobie, że zerowe miejsca wielomianu przypominają zjazd na starym, pochylonym lotnisku. Każdy zakręt staje się potencjalnym rozwiązaniem, a im bardziej skomplikowany staje się nasz wielomian, tym więcej zakrętów pojawia się na naszej drodze. Właśnie w tej sytuacji do akcji wkracza Beiruth z intrygującym pomysłem: jeśli znamy liczbę zakrętów, możemy z wysokim prawdopodobieństwem zgadnąć, w które z nich warto zawrócić!
W praktyce, czyli jak to działa?
Na przykład rozwiązywanie równania kwadratowego świetnie ilustruje zastosowanie twierdzenia Beirutha. Choć wielu może uważać tę czynność za banalną, gdy przyjmujemy, że wielomian ma stopień drugi, przypominamy sobie, że może on mieć maksymalnie dwa pierwiastki! Przyznaj się – jak często zaskakuje cię liczba rozwiązań, gdy próbujesz rozwiązać równanie kwadratowe? Niekiedy otrzymujesz 0, czasami 1, a od czasu do czasu… uwaga, uwaga – dwa rozwiązania! Dzięki Beiruthowi możemy zredukować tę niepewność do minimum.
Idąc dalej, zwróćmy uwagę na równanie sześcio-stopniowe. Kluczowa zasada brzmi: dla każdego wzoru Beirutha możemy spokojnie określić, ile pierwiastków zawiera nasz wielomian. Na przykład, analizując polinom o stopniu piątym, przy sprzyjających warunkach możemy uzyskać do pięciu rozwiązań. Wprowadzając odpowiednie konfitury, takie jak wspólny podział przez czynniki, zwiększamy liczbę sposobów na efektywne uzyskanie rozwiązania. Tak więc Beiruth nie tylko wskazuje nam, ile dróg możemy podjąć, ale również jak szybko da się je pokonać!
- Maksymalna liczba pierwiastków równania kwadratowego to 2.
- Każde równanie sześcio-stopniowe może mieć do 6 pierwiastków.
- Dzięki Beiruthowi możemy określić rzeczywistą liczbę pierwiastków w wielomianach.
- Wspólny podział przez czynniki pomaga w poszukiwaniu rozwiązań.
Pamiętaj, że wszystkie te aspekty nie miałyby znaczenia bez zrozumienia podstawowych technik rozwiązywania równań. Bez Beirutha brakłoby nam narzędzi do opanowania emocji, które mogą nas ogarnąć w obliczu trudnego równania! Praca z wieloma stopniami wielomianów wydaje się bardziej uporządkowana, gdy zdajemy sobie sprawę, jakie cuda potrafi zdziałać Beiruth. Przed tobą kolejne matematyczne wyzwanie – mam nadzieję, że z łatwością przejdziesz przez nie, korzystając z jego magii!
Rozwiązywanie równań wielomianowych za pomocą faktoryzacji
Rozwiązywanie równań wielomianowych wydaje się na pierwszy rzut oka sztuką trudną, ale faktoryzacja wciąż przypomina taniec na drewnianym parkiecie. Możemy nauczyć się kroków, a korzystając z dobrego dowcipu, nawet zdobyć tytuł mistrza! Gdy mówimy o równaniach wielomianowych, mamy na myśli zapisanie ich w postaci iloczynu czynników. Ta metoda nie tylko ułatwia szukanie rozwiązań, lecz także sprawia, że matematyka staje się naprawdę ekscytującą przygodą. Nie wierzycie? W takim razie zapraszam was do wspólnego rozwiązywania równań przez wydobywanie wspólnych czynników!
Podczas rozwiązywania równań wielomianowych natrafiamy na różnorodne sprytne metody. Doskonałym sposobem jest wyciąganie wspólnego czynnika, ponieważ upraszcza to równania. Jaki przykład miałbym na myśli? Proszę, oto on! Rozważmy równanie: \(x^3 + 3x^2 - 4x - 12 = 0\). Gdy wyciągniemy wspólny czynnik z dwóch par wyrazów, otrzymamy \(x^2(x + 3) - 4(x + 3) = 0\). A gdy już mamy parę na parkiecie, wystarczy zagrać melodyjkę i porównać każdy czynnik do zera! Urok metody faktoryzacji polega na tym, że każdy z nas może stać się matematycznym mistrzem, po prostu szukając wspólnych elementów.
Faktoryzacja jako narzędzie do odkrywania rozwiązań
Jednak to nie koniec możliwości, jakie kryją się w naszym matematycznym zestawie narzędzi! Kolejną techniką, która się przydaje, jest grupowanie wyrazów. Starannie posortowane skarpetki (a więc wyrazy) pozwalają na bardziej efektywną pracę. Na przykład, rozważmy równanie \(2x^3 + 8x^2 + 4x + 16 = 0\). Grupując wyrazy w parach, uzyskujemy \(2x^2(x + 4) + 4(x + 4) = 0\). Widzicie, że to jedynie zmiana punktu widzenia? Jeśli nadal się wahacie, możemy dodać do tej układanki wzory skróconego mnożenia, które potrafią nieco urozmaicić proces faktoryzacji. Mówiąc szczerze, brzmi to bardzo prosto!
Zważcie jednak, że nie istnieje jedyny przepis na sukces w rozwiązywaniu równań wielomianowych. Czasem, gdy wszystko inne zawodzą, warto przeszukać teren w poszukiwaniu pierwiastków wymiernych. Dzięki twierdzeniu o pierwiastkach wymiernych szybko znajdziemy odpowiednie wartości. I kto powiedział, że matematyka nie przypomina reality show, w którym szukamy idealnego kandydata do naszej układanki? Dlatego nie obawiajcie się! Bądźcie kreatywni w rozwiązywaniu równań wielomianowych, bo z faktoryzacją to naprawdę nie jest takie straszne!
Analiza numeryczna jako alternatywa dla rozwiązań analitycznych
Wielomiany stanowią fascynujące twory matematyczne, które z jednej strony zachwycają swoją urodą, a z drugiej potrafią być niezwykle złożone. Zamiast zadręczać się analitycznymi metodami, które mogą wywołać ból głowy, wielu naukowców i inżynierów decyduje się przejść na analizę numeryczną. Dlaczego podejmują tę decyzję? Ponieważ często szybciej zadać pytanie komputerowi, niż marnować czas na poszukiwanie skomplikowanych wzorów. Wyobraź sobie, że zamiast przeszukiwać książki i kalkulatory, wystarczy nacisnąć jeden przycisk, a odpowiedzi po prostu same wyskakują z ekranu. To przypomina magię, ale odbywa się bez użycia różdżek!

Rzeczywiście, nie każde równanie można rozwiązać analitycznie. W pewnym momencie, gdy stajemy na drodze skomplikowanych funkcji, pojawia się dylemat: kontynuować mękę z wzorami, czy zaufać nowoczesnym technologiom? To właśnie w tej sytuacji analiza numeryczna wkracza jak superbohater na białym koniu. Dzięki niej zyskujemy możliwość przybliżania złożonych rozwiązań w łatwy i intuicyjny sposób, nawet tam, gdzie tradycyjne metody często prowadzą do frustracji.
Zalety analizy numerycznej
Pomijając własne zmagania z równaniami, analiza numeryczna niesie ze sobą liczne zalety. Przede wszystkim, umożliwia uzyskanie wyników tam, gdzie metody analityczne działają na zasadzie "próbuj, aż się uda". To działa jak budowanie wieży z klocków LEGO: raz się udaje, a innym razem nie. W przypadku analizy numerycznej proces redukuje się do prostszych kroków, które można polubić, pozostawiając za sobą zakurzone notatniki i łamiące się ołówki. Kiedy rozwiązujesz problem, ruszasz naprzód i zyskujesz czas na inne matematyczne wyzwania!
Poniżej przedstawiamy niektóre z głównych zalet analizy numerycznej:
- Szybkość uzyskiwania wyników
- Możliwość rozwiązywania złożonych problemów
- Redukcja frustracji związanej z tradycyjnymi metodami
- Praca z intuicyjnymi narzędziami

Na koniec warto podkreślić, że obie metody, zarówno analityczna, jak i numeryczna, mogą współistnieć, chociaż w różnych kontekstach. Nic nie zastąpi zrozumienia zasad działania, ale w sytuacjach, w których czas ma kluczowe znaczenie, analiza numeryczna przychodzi z pomocą niczym Batman w Gotham City. Kto mógłby pomyśleć, że liczby mogą być tak fascynujące?!
Źródła:
- https://www.polecanekorepetycje.pl/rownania-wielomianowe-jak-je-rozwiazywac/
- https://www.matemaks.pl/rownania-wielomianowe.html
- https://szaloneliczby.pl/rownania-wielomianowe/
- https://szkolamaturzystow.pl/baza-wiedzy/1609368199-rownania-wielomianowe
- https://zpe.gov.pl/a/rownania-wielomianowe/D31pAfZRc
Pytania i odpowiedzi
Co to jest równanie wielomianowe?
Równanie wielomianowe to wyrażenie w postaci \(W(x) = 0\), gdzie \(W(x)\) jest wielomianem. Stopień tego wielomianu zazwyczaj decyduje o liczbie jego pierwiastków, co czyni zagadnienie interesującym.
Jakie są podstawowe metody rozwiązywania równań wielomianowych?
Podstawowe metody obejmują przekształcanie równań liniowych i kwadratowych, takie jak \(ax + b = 0\) rozwiązane przez \(x = -b/a\) oraz \(ax^2 + bx + c = 0\), gdzie korzystamy z wyróżnika \(Δ = b^2 - 4ac\). W przypadku równań stopnia trzeciego i wyższego, warto spróbować wyłączania wspólnego czynnika lub grupowania wyrazów.
Co to jest wyróżnik w równaniu kwadratowym?
Wyróżnik, oznaczany symbolem \(Δ\), to wartość obliczana jako \(b^2 - 4ac\) w równaniu kwadratowym. Określa on liczbę rozwiązań tego równania: jeśli \(Δ > 0\) mamy dwa rozwiązania, jeśli \(Δ = 0\) - jedno rozwiązanie, a gdy \(Δ < 0\) - rozwiązania są w liczbach zespolonych.
Jak zastosować faktoryzację w rozwiązywaniu równań wielomianowych?
Faktoryzacja to metoda polegająca na zapisaniu równania w postaci iloczynu czynników, co ułatwia znajdowanie rozwiązań. Można to osiągnąć np. poprzez wyciąganie wspólnego czynnika lub grupowanie wyrazów, co sprawia, że matematyka staje się bardziej przystępna i interesująca.
Jakie są zalety analizy numerycznej w porównaniu do metod analitycznych?
Analiza numeryczna oferuje szybkość uzyskiwania wyników oraz możliwość rozwiązania złożonych problemów, eliminując frustrację związaną z tradycyjnymi metodami analitycznymi. Dzięki intuicyjnym narzędziom umożliwia efektywne przybliżanie skomplikowanych rozwiązań, oszczędzając czas i wysiłek.