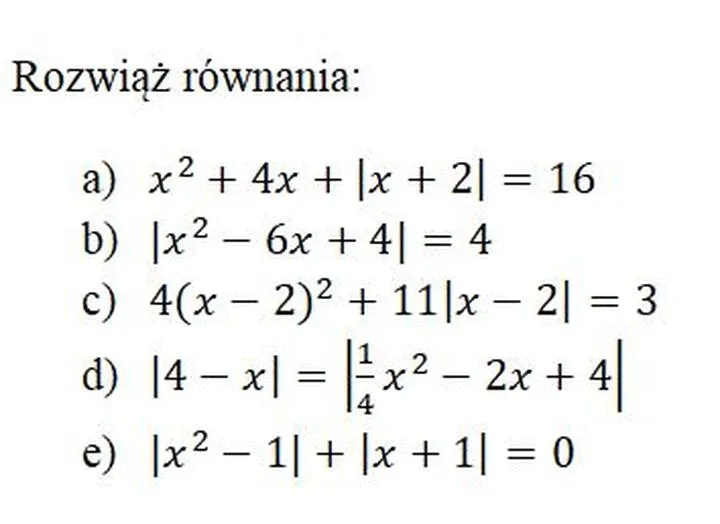Nie ma co ukrywać – równania z wartością bezwzględną mogą przyprawić o zawrót głowy, a ich zrozumienie wymaga nieco wysiłku. Mimo że na pierwszy rzut oka wydają się niepozorne, potrafią zaskoczyć nas jak nieproszony gość na przyjęciu. Wartość bezwzględna oznacza nic innego jak odległość danej liczby od zera na osi liczbowej, co stanowi pierwszy klucz do zrozumienia całego tematu. Jednak że to tylko początek. Oprócz znajomości definicji, musimy także zdobyć umiejętności przekształcania równań oraz myślenia w różnych przypadkach. Już wiemy, że wartość bezwzględna liczby 5 wynosi 5, a wartość bezwzględna liczby −5 również daje nam 5. Cóż za sprytnie brzmiąca powtórka!
- Wartość bezwzględna wyraża odległość liczby od zera na osi liczbowej.
- Rozwiązując równania z wartością bezwzględną, należy rozważyć dwa przypadki: jeden z dodatnim, drugi z ujemnym znakiem.
- Wartość bezwzględna nigdy nie może przyjmować wartości ujemnych.
- Kluczowe jest przekształcanie równania przed jego rozwiązaniem, co ułatwia obliczenia.
- Pomijanie warunków rozwiązania prowadzi do błędnych wyników – wartość bezwzględna zawsze jest nieujemna.
- Uważność na liczby ujemne po prawej stronie równania jest istotna, aby uniknąć sytuacji bez rozwiązania.
- Równania z wartością bezwzględną mają praktyczne zastosowania w codziennym życiu, takie jak analiza cen czy ustalanie odległości między miejscami.
Absolutnie kluczowe jest zdobycie jasnej idei, że kiedy mamy równanie w stylu \(|x+3|=5\), nasze odpowiedzi będą wynikały z dwóch rzeczywistych scenariuszy: pierwszego \(x+3=5\) oraz drugiego \(x+3=-5\). W tym przypadku układamy prawdziwe puzzle, a nasze umiejętności szukania rozwiązań decydują o sukcesie. Tak więc rozbieżności kosztują nas tylko dodatkowy wysiłek, a nie obniżają oceny na teście!
Wartość bezwzględna w akcji
Nie zapominajmy, że wartości bezwzględne potrafią być kapryśne. Ich prawidłowe zastosowanie w równaniach wymaga od nas przemyślenia. Gdy już mamy nasze równanie, możemy bez trwogi rozbić je na dwa: jedno z dodatnim znakiem, drugie z ujemnym. Równanie \(|2x+3|=7\) przekształca się z łatwością w dwa: \(2x+3=7\) oraz \(2x+3=-7\). Widzisz? Formuła okazuje się prosta, a praktyka sprawia, że staje się coraz łatwiejsza, niczym gra, której zasady znamy na pamięć.
Spróbujmy jeszcze w sposób przewrotny: wyobraziliśmy sobie, że równanie \(|x|=-2\) istnieje. Mówmy to głośno – takie równanie istnieje tylko w fantazjach matematyka, ponieważ wartość bezwzględna nigdy nie przyjmuje wartości ujemnych! To podobne do próby wyciśnięcia pieska z kontenera na cukierki. Dlatego zrozumienie wartości bezwzględnej stanowi klucz do skutecznego rozwiązywania równań. Szybciej, niż się spodziewasz, możesz zdobyć nowe umiejętności, które uczynią z ciebie matematycznego czarodzieja! Wystarczy trochę praktyki, a możesz nawet stać się mistrzem wartości bezwzględnej w swoim kręgu znajomych – a to, przyznam, brzmi całkiem fajnie!
Najczęstsze pułapki przy rozwiązaniu równań z wartością bezwzględną – jak ich unikać?
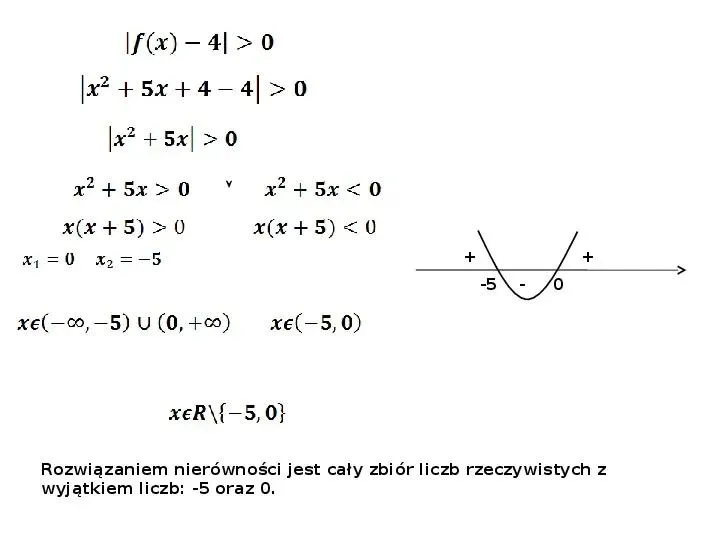
Rozwiązywanie równań z wartością bezwzględną to prawdziwa matematyczna kąpiel! W tej dziedzinie odnajdziesz zarówno radość, jak i niebezpieczne głębiny, w które łatwo wpaść. Weźmy na przykład równanie \(|x+3|=5\). Na pierwszy rzut oka wygląda ono łagodnie, jak letnia bryza. Jednak, jak to często bywa, w tej sytuacji pojawiają się pułapki! W tym przypadku mamy dwie możliwości: \(x+3=5\) lub \(x+3=-5\). Niespodzianka! Oznacza to, że aż dwa rozwiązania czekają na wyciągnięcie ręki, co możesz uznać za pierwszy krok do rozpracowania tego skomplikowanego matematycznego problemu.
Na co uważać podczas rozwiązywania równań?
Jednakże, aby odnieść sukces, nie daj się zwieść i zawsze bądź czujny! Pułapką numer dwa, którą warto wymienić, jest największy grzech – pomijanie warunków rozwiązania! Weź to sobie do serca, bo jeżeli po lewej stronie równania znajduje się wartość bezwzględna, a po prawej liczba ujemna, to sytuacja kończy się na zbiorze pustym. Pamiętaj, wartość bezwzględna zawsze pozostaje nieujemna. Gdyby to było takie proste, każdy mógłby zostać matematykiem, a my wszyscy z łatwością zdawalibyśmy wszystkie egzaminy!
W rozwiązywaniu zagadek z wartością bezwzględną liczy się też umiejętność przekształcania równań. Czasami, zamiast od razu dzielić na dwa równania, warto najpierw uprościć zapis. Na przykład, analizując równanie \(4+|x+3|=15\), najpierw pozbądź się liczby cztery i przekształć je do formy \( |x+3|=11\). Angażując się w te praktyczne przekształcenia, zyskasz nie tylko lepszą orientację, ale także zaoszczędzisz cenny czas podczas egzaminów.
Oto kilka kluczowych zasad, o których warto pamiętać przy rozwiązywaniu równań z wartością bezwzględną:
- Nie pomijaj warunków rozwiązania.
- Wartość bezwzględna zawsze jest nieujemna.
- Przekształcaj równania przed ich rozwiązaniem.
- Uważaj na liczby ujemne po prawej stronie równania.
Równania z wartością bezwzględną mogą dostarczać zabawy i zaskoczeń, ale kluczowe staje się przestrzeganie zasady: Kajam się, gdy nie zauważę warunków. Zawsze przypominaj sobie, że coś, co wydaje się ciekawe, nie zawsze jest łatwe do zrealizowania. A zatem do dzieła – wspaniałe rozwiązania czekają właśnie na Ciebie!
| Pułapka | Opis | Jak unikać |
|---|---|---|
| Pomijanie warunków rozwiązania | Nie uwzględnianie warunków, co prowadzi do błędnych rozwiązań. | Zawsze sprawdzaj, czy rozwiązanie jest zgodne z warunkami równania. |
| Wartość bezwzględna jest nieujemna | Wartość bezwzględna nie może być równa liczbie ujemnej. | Uważaj przy rozwiązywaniu równań z wartościami ujemnymi po prawej stronie. |
| Przekształcanie równań | Rozpoczynanie rozwiązania bez wcześniejszego uproszczenia równania. | Uprość równanie przed jego rozwiązaniem, aby zaoszczędzić czas. |
| Uważność na liczby ujemne | Nie zwracanie uwagi na liczby ujemne po prawej stronie równania. | Analizuj każdą stronę równania, aby uniknąć błędów. |
Ciekawostką jest, że wartości bezwzględne można interpretować geograficznie – na osi liczbowej przedstawiają one odległość od zera, niezależnie od kierunku, co w praktyce oznacza, że równanie z wartością bezwzględną może mieć więcej niż jedno rozwiązanie, jeśli przekształcisz je prawidłowo!
Krok po kroku: Praktyczne metody rozwiązania równań z wartością bezwzględną
Rozwiązywanie równań z wartością bezwzględną nie jest wcale tak trudne, jak może się wydawać! Klucz do sukcesu polega na zrozumieniu, co dokładnie oznacza wartość bezwzględna. Mówiąc najprościej, wartość bezwzględna liczby określa jej odległość od zera na osi liczbowej. Weźmy przykład: wartość bezwzględna liczby pięć wynosi pięć, natomiast wartość bezwzględna liczby minus pięć? Również pięć! Czyż to nie jest fascynujące? Zanim jednak przejdziemy do rozwiązywania równań, musimy pamiętać, że wartości bezwzględne dają nam możliwość poszukiwania dwóch rozwiązań, bo w matematyce „minus” ma równie dużą wagę co „plus”!
Kluczowe kroki w rozwiązywaniu równań z wartością bezwzględną
Teraz przystąpmy do działania! Kiedy napotykasz równanie w formie |x + 3| = 5, powinieneś rozważyć dwa przypadki. Z jednej strony, istnieje sytuacja, w której x + 3 = 5, a z drugiej, można mieć x + 3 = -5. Prosto, prawda? Po przekształceniu tych równań uzyskujesz dwie wartości x, które stanowią Twoje rozwiązania. Takie podejście to niezawodny przepis na osiągnięcia w matematyce! Równania z wartością bezwzględną przypominają swoistą grę w „dwie prawdy”, więc warto odnaleźć się w tej zabawie.
Nie daj się zaskoczyć!

Zawsze pamiętaj, aby sprawdzać, czy po wykonaniu obliczeń spełniasz warunki równań. Ponadto czasami wystarczy, by pozbyć się wartości bezwzględnej, aby uprościć równanie, na przykład w przypadku |4x + 8| = 0. Tutaj warto zauważyć, że równania z wartością bezwzględną nie akceptują liczb ujemnych po prawej stronie, ponieważ... cóż, nikt ich nie zaprasza! Brak rozwiązań oznacza, że nie istnieje wartość x, która spełniałaby takie hipotetyczne warunki. Aby unikać pułapek matematycznych niuansów, zawsze bądź czujny!
Na koniec nie zapominaj, że wartość bezwzględna przydaje się nie tylko podczas rozwiązywania równań, ale także w codziennym życiu. To jak mówić w liczbach: „Bez względu na to, czy jesteś szczęśliwy, czy smutny, i tak zawsze wracasz do zera!” A więc z każdą rozwiązana zagadką stajesz się mądrzejszy i pewniejszy swoich matematycznych umiejętności, zatem trzymaj się swojej kalkulatorowej broni i do dzieła! Matematyka to zabawa!
Przykłady z życia wzięte: Zastosowanie równań z wartością bezwzględną w codziennych problemach
Równania z wartością bezwzględną to jeden z tych tematów, które potrafią zjeżyć włosy na głowie nawet najbardziej zrelaksowanym uczniom. Jak to możliwe, że jedna liczba ma dwa oblicza? W końcu wartość bezwzględna to nic innego jak odległość od zera na osi liczbowej, ale kiedy przystępujemy do rozwiązywania równań, to magia zaczyna działać. Weźmy na przykład równanie tak proste jak \(|x - 2| = 5\). Gdyby x był w klubie, miałby dwa zaproszenia: na 7 i -3. Tak, dokładnie tak! Wszystko sprowadza się do analizy i przekształcania równań, co jest naprawdę ekscytujące!
Odkrywając, że równania z wartością bezwzględną czają się nie tylko w podręcznikach matematycznych, ale także w naszym codziennym życiu, zaczynamy dostrzegać ich różnorodne zastosowania. Wyobraź sobie, że planujesz zakup nowego smartfona, ale chcesz najpierw zrozumieć różnicę między ceną rynkową a ceną w sklepie. Możesz zapisać to jako równanie z wartością bezwzględną: \(|cena\_rynkowa - cena\_sklepu| = różnica\_cen\). Taki zapis nie tylko ułatwi zakupy, ale także pomoże ci wytłumaczyć mamie, dlaczego wydajesz pieniądze na nowinki technologiczne!
Równania w praktyce
Nie da się ukryć, że matematyczne potwory, jakimi są równania z wartością bezwzględną, pojawiają się również w nietypowych sytuacjach. Na przykład, wyobraź sobie, że musisz dojść do porozumienia z przyjacielem, ustalając miejsce spotkania. Równanie \(|x - 3| = 2\) może być doskonałym przykładem, ponieważ oznacza, że oboje znajduje się w odległości 2 od punktu, który stanowi kompromis. Czy umówicie się w parku? A może w kawiarni? Matematyka wnika w nasze życie codzienne, nawet gdy tego nie zauważamy.
Oto kilka sytuacji, w których równania z wartością bezwzględną mogą być użyteczne:
- Ustalanie odległości między miejscami spotkań.
- Obliczanie różnicy cen w zakupach.
- Analiza błędów pomiarowych w eksperymentach.
- Ocena różnic w wynikach testów.
Równania z wartością bezwzględną pełnią rolę pewnego rodzaju języka, który pozwala nam opisywać otaczający świat w sposób zrozumiały i logiczny. Umiejętność rozwiązywania tych równań warto opanować, aby lepiej radzić sobie nie tylko na egzaminach, ale również w codziennych sytuacjach. Może następnym razem, gdy złapiesz się na liczeniu potencjalnych punktów za sprytne argumenty podczas zakupów, pomyśl o tym, jakie równanie mogłoby pomóc ci znaleźć właściwą wartość bezwzględną w tej sytuacji. Matematyka to nie tylko nudna teoria, lecz także narzędzie do zrozumienia świata, w którym żyjemy!