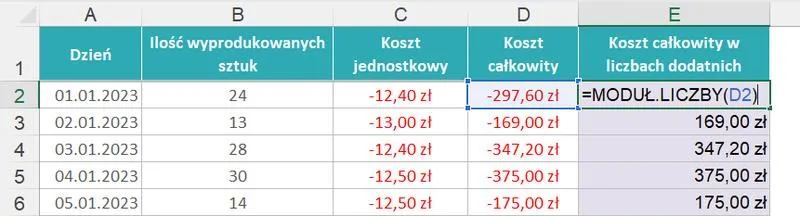
Trójkąt równoramienny to geometryczna figura, która często pojawia się w naszych myślach, szczególnie podczas wykonywania zadań matematycznych w szkole. Dlatego warto pamiętać, że pole tego trójkąta można obliczać na kilka różnych sposobów, co zależy od danych, które posiadamy. Gdy dysponujemy długością podstawy oraz wysokością, możemy skorzystać z najprostszego wzoru: \(P = \frac{1}{2} a h\). W tej formule 'a' oznacza długość podstawy, a 'h' wskazuje wysokość opuszczoną na nią. Z pewnością każdy nauczyciel matematyki odczuje satysfakcję, gdy uczeń potrafi odpowiedzieć, używając tego wzoru!
- Trójkąt równoramienny można obliczać na kilka różnych sposobów w zależności od danych.
- Podstawowy wzór na pole trójkąta to \(P = \frac{1}{2} a h\), gdzie 'a' to długość podstawy, a 'h' to wysokość.
- Wysokość można wyliczyć z twierdzenia Pitagorasa, jeśli znamy długość ramion.
- Inne metody obliczania pola to wykorzystanie kątów oraz wzór Herona.
- Geometria jest kluczowa dla zrozumienia przestrzeni i obliczeń pól różnych figur.
- W obliczeniach warto pamiętać o najczęstszych błędach, takich jak zapominanie o wysokości czy mylenie wzorów.
- Zastosowanie wzoru Pitagorasa ułatwia obliczenie wysokości w trójkącie równoramiennym.
Wysokość w trójkącie równoramiennym
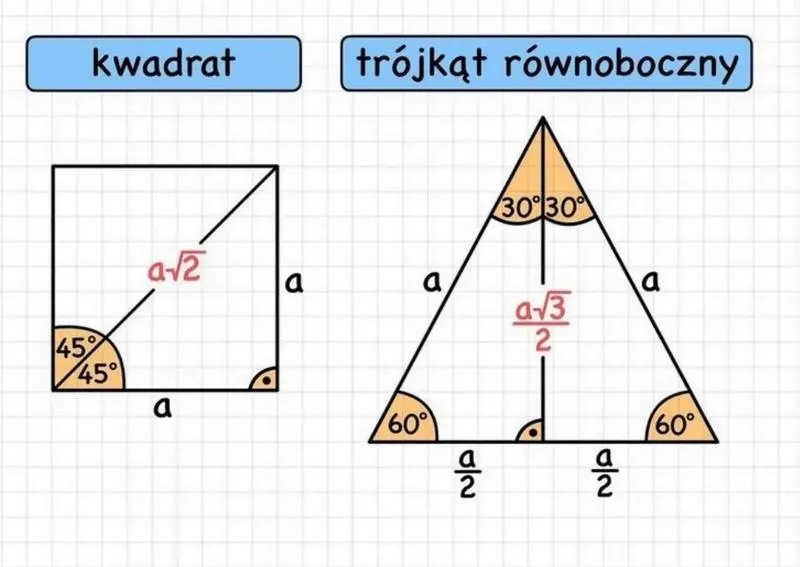
Warto zauważyć, że nie zawsze otrzymujemy wszystkie potrzebne dane od razu; czasami konieczne jest wyliczenie wysokości z innych elementów trójkąta. Gdy znamy długość ramienia (boku o równej długości), możemy wykorzystać twierdzenie Pitagorasa. W takim przypadku wysokość dzieli trójkąt na dwa przystające trójkąty prostokątne. Jeśli pamiętasz, że ramiona mają długość 'b', a podstawa 'a', możemy użyć równania \(b^2 = h^2 + \left(\frac{a}{2}\right)^2\) do obliczenia wysokości, co daje \(h = \sqrt{b^2 - \left(\frac{a}{2}\right)^2}\). Proste i przyjemne, prawda? Już teraz widać, jak matematyka staje się coraz mniej przerażająca!
Inne metody obliczania pola
Nie sposób zapomnieć o dodatkowych sposobach, które również możemy wykorzystać! Na przykład, jeśli dysponujemy informacjami o dwóch bokach trójkąta oraz kącie między nimi, mamy wzór: \(P = \frac{1}{2} c d \sin \gamma\). W kontekście trójkąta równoramiennego, gdzie ramiona mają długość 'b', pole wyraża się jako: \(P = \frac{1}{2} b^2 \sin \alpha\). Z kolei bardziej zaawansowani matematycy mogą sięgnąć po wzór Herona, który wymaga jedynie znajomości długości wszystkich boków i wygląda następująco: \(P = \sqrt{p(p - a)(p - b)(p - c)}\), gdzie \(p\) oznacza półobwód. Jak widać, pole trójkąta równoramiennego można zapisać na wiele sposobów, a każdy z nich jest równie ważny jak ulubiony przepis na pyszne ciasto!
Zastosowanie zasad geometrii w obliczeniach pola
Geometria stanowi znacznie więcej niż tylko zbiór nudnych regułek oraz wzorów; to klucz do odkrywania tajemnic przestrzeni, w której na co dzień się poruszamy. Przykładem jej zastosowania, które łatwo można zrozumieć, jest obliczanie pola różnorodnych figur, w tym trójkątów. Dzięki kilku prostym wzorom, nawet osoba, która nie zna się na matematyce, z łatwością przeliczy pole trójkąta. Wystarczy jedynie znać długość podstawy oraz wysokość. Dodatkowo można wprowadzić nieco zawirowania, dodając różne dane, takie jak długości ramion czy kąty. Ostatecznie, kto nie doceni odrobiny matematycznego szaleństwa?
Jakie wzory pomagają w obliczeniach?
Warto zapamiętać podstawowy wzór na pole trójkąta, niczym tekst ulubionej piosenki, polegający na pomnożeniu długości podstawy przez wysokość, a następnie podzieleniu przez dwa. Jednak to zaledwie początek! Kiedy trójkąt zachwyca równoramiennością, możemy skorzystać z twierdzenia Pitagorasa, które sprawia, że wysokość przestaje być tylko teoretycznym pojęciem, stając się realnym elementem, który łatwo obliczyć. Dlatego zamiast czuć się przytłoczonym liczbami, przekształcamy skomplikowane zbiory danych w proste wyrażenia, co pozwala nam na wyjście z matematycznego labiryntu.
Co z innymi figurami?
Nie możemy zapominać, że geometria przybiera wiele różnych form! Możemy także bawić się wzorami, zestawiając długości boków oraz kąty. W tym przypadku musimy sięgnąć do wzoru, który przypomina nam, że do obliczenia pola potrzebujemy nie tylko długości, ale również kątów! Dzięki takim operacjom otwierają się przed nami nowe horyzonty, gdy zaczynamy pełnić rolę prawdziwego geometra – nie tylko z mapą w dłoni, ale również z konturami, które przekształcają się w pole, gotowe do zmierzenia.
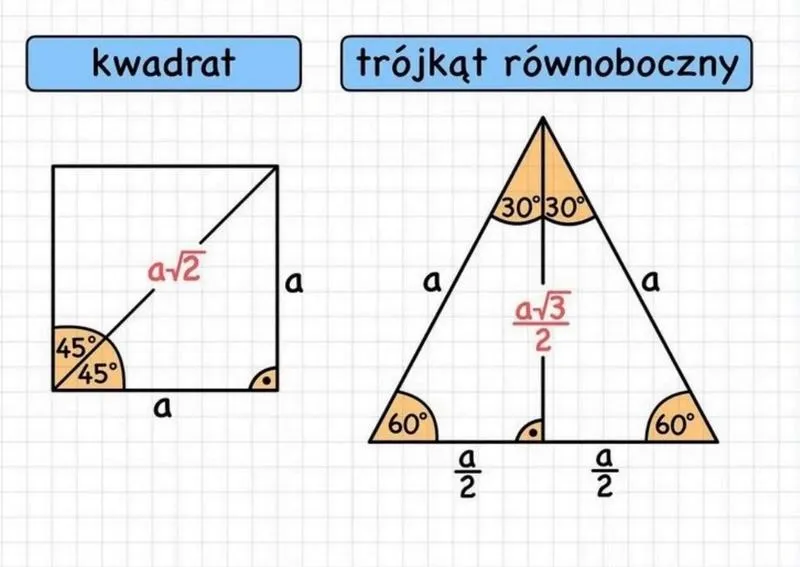
Oto kilka przykładów figur, których pole możemy obliczyć:
- Kwadrat - pole obliczamy jako długość boku podniesioną do kwadratu.
- Prostokąt - pole to iloczyn długości i szerokości.
- Trapez - pole obliczamy na podstawie podstaw i wysokości poprzez wzór (a+b)*h/2.
- Koło - pole wyznacza się ze wzoru πr², gdzie r to promień.
Wiemy dobrze, że matematyka nie zawsze okazywała się naszym najlepszym przyjacielem. Niemniej jednak, dzięki kilku prostym zasadom geometrii, zyskujemy możliwość zgłębienia tajemnic trójkątów oraz innych figur, a także odkrywania radości w poznawaniu, jak świat wokół nas można opisać za pomocą tej pięknej nauki. Zatem do dzieła! Nadszedł czas, aby zadawać nowe pytania i obliczać to, co wcześniej wydawało się niemożliwe!
Praktyczne przykłady obliczania pola trójkąta równoramiennego
Obliczanie pola trójkąta równoramiennego przypomina składanie Lego – z pozoru proste, ale w rzeczywistości wymaga sprytu oraz przemyślanej strategii. Zaczynając od podstaw, przypomnijmy sobie fundamentalny wzór, który stwierdza, że pole trójkąta to połowa podstawy pomnożona przez wysokość. Porównując to do gotowania, zamiast mąki mamy długość boku, oznaczaną jako „a”, natomiast wysokość, która opada na ten bok, możemy nazwać „h”. Formuła jest prosta i zrozumiała: \( P = \frac{1}{2} \cdot a \cdot h \). I gotowe! Posiadając te dwa składniki, możemy z łatwością obliczyć pole trójkąta.
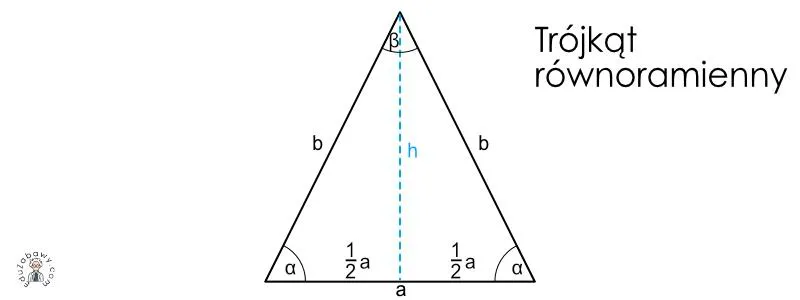
Przechodząc dalej, wysokość można znaleźć dzięki twierdzeniu Pitagorasa. Wyobraź sobie sytuację, w której wysokość, ramię i połowa podstawy tworzą trójkąt prostokątny. I oto rozwiązanie: wysokość „h” można obliczyć za pomocą wzoru \( h = \sqrt{b^2 - \left(\frac{a}{2}\right)^2}\), gdzie „b” oznacza długość ramion trójkąta. Następnie, przy użyciu znanych przepisów, możemy bez trwogi obliczyć pole! Teraz czas na konkretne przykłady, które przyciągną naszą uwagę.
Jak skutecznie obliczyć pole - przykłady w praktyce
Nie zapominajmy także o wzorze Herona, który umożliwia obliczenie pola tylko na podstawie długości boków. Jak widać, liczby są wyjątkowo elastyczne, a my musimy umiejętnie nimi zarządzać.
Na koniec zaskoczeniem może być pytanie: „Czy te boki mogą tworzyć trójkąt równoramienny?”. Nigdy nie zapominaj o złotej zasadzie: suma długości dwóch boków zawsze musi być większa od długości trzeciego. To jak granice zdrowego rozsądku. Jeśli boki spełniają tę zasadę, to czas na zabawę – możemy przystąpić do obliczania pola, a jeśli nie, to musimy ustawić się w kolejce i poczekać na dalsze kroki! Tak to właśnie działa w przypadku trójkątów – wesoła matematyka, która staje się przyjemnością, jeśli tylko zachowamy dobry humor.
| Metoda | Opis | Wzór |
|---|---|---|
| Podstawa i wysokość | Obliczanie pola na podstawie długości podstawy i wysokości. | P = (1/2) * a * h |
| Twierdzenie Pitagorasa | Obliczanie wysokości na podstawie długości ramion i podstawy. | h = √(b² - (a/2)²) |
| Wzór Herona | Obliczanie pola trójkąta na podstawie długości wszystkich boków. | P = √(s * (s-a) * (s-b) * (s-c)), gdzie s = (a + b + c) / 2 |
Najczęstsze błędy przy obliczaniu pola trójkąta równoramiennego
Kiedy myślisz o trójkącie równoramiennym, pewnie wyobrażasz sobie idealnie symetryczny kształt. Warto jednak pamiętać, że jednym z najczęstszych problemów podczas obliczania jego pola jest zapominanie o podstawowej zasadzie: dobry wzór działa jak klucz! Nie wystarczy jedynie przypomnieć sobie formułę z pamięci. Zamiast tego, upewnij się, że masz właściwe dane. Najczęściej zapominamy o wysokości, co prowadzi nas na manowce w obliczeniach. Wysokość to ten szanowany gość, bez którego nasze obliczenia zamieniają się w jeden wielki, matematyczny chaos!
Wzory na pole trójkąta równoramiennego – nie bądź jak Krysia z szachownicą!
Niektóre osoby, a może Krystyna, mylą wzory i zamiast stosować odpowiednią formułę, próbują kombinować, niechcący eliminując potrzebę wysokości. Czasami obliczają pole, używając boku czy kąta, podczas gdy lepszym rozwiązaniem stosowanie wzoru opartego na podstawie i wysokości. Zamiast skomplikowanych wyliczeń z użyciem sinusów, najpierw lepiej wyliczyć wysokość. Nie ma nic gorszego niż uczucie, że zaraz zostaniesz zaproszony na matematykę przy tablicy, z pustą dłonią w kieszeni!
Na koniec, pamiętajmy również o dwóch bokach! Jeśli pragniesz zabawić się w liczenie boku przy użyciu twierdzenia Pitagorasa, upewnij się, że nie zagubisz się w zawirowaniach długości ramion i podstawy. Wiele osób zapomina, że aby wyciągnąć wysokość z ramion, najpierw trzeba podzielić podstawę na dwie równe części. Dzięki temu utworzymy trójkąty prostokątne, które udzielą nam dwóch cennych odpowiedzi: ciepły uśmiech oraz pole trójkąta! Niech Twoje obliczenia zawsze będą jasne i proste, jak trójkąt równoramienny!
Oto kilka kluczowych zasad, o których warto pamiętać przy obliczaniu pola trójkąta równoramiennego:
- Upewnij się, że znasz długość podstawy.
- Wylicz wysokość na podstawie ramion i podstawy.
- Stosuj odpowiednią formułę do obliczeń.
- Nie zapominaj o tym, aby podzielić podstawę na dwie równe części przy wyliczaniu wysokości.
Źródła:
- https://szkolazklasa20.pl/pole-trojkata-rownoramiennego-wzory-i-zadania-z-rozwiazaniami/
- https://www.matemaks.pl/wzory-na-pole-trojkata.html
- https://zpe.gov.pl/a/pole-trojkata/D1011a4cs
Pytania i odpowiedzi
Jakie są podstawowe dane potrzebne do obliczenia pola trójkąta równoramiennego?
Aby obliczyć pole trójkąta równoramiennego, potrzebujemy długości podstawy ('a') oraz wysokości ('h') opuszczonej na tę podstawę. Możemy skorzystać z wzoru: \(P = \frac{1}{2} a h\).
Jak można obliczyć wysokość trójkąta równoramiennego, gdy znana jest długość ramion?
Wysokość trójkąta równoramiennego można obliczyć, korzystając z twierdzenia Pitagorasa. Gdy znamy długość ramienia ('b') i podstawy ('a'), stosujemy wzór: \(h = \sqrt{b^2 - \left(\frac{a}{2}\right)^2}\).
Jakie są inne metody obliczania pola trójkąta równoramiennego?
Można również obliczyć pole trójkąta równoramiennego, korzystając z wzoru na podstawie długości dwóch boków i kąta między nimi: \(P = \frac{1}{2} c d \sin \gamma\). Alternatywnie, wzór Herona pozwala obliczyć pole, znając długości wszystkich boków.
Czy istnieją najczęstsze błędy popełniane przy obliczaniu pola trójkąta równoramiennego?
Najczęściej spotykanym błędem jest zapominanie o wysokości, co prowadzi do błędnych obliczeń. Ważne jest również, by stosować odpowiednie wzory oraz upewnić się, że mamy wszystkie potrzebne dane.
Co powinno się pamiętać przy stosowaniu wzoru Pitagorasa do obliczenia wysokości?
Podczas korzystania z wzoru Pitagorasa, należy pamiętać, aby podzielić długość podstawy na dwie równe części. To pozwoli utworzyć trójkąty prostokątne, z których łatwo można wyliczyć wysokość.